ここまで来ると、貴方にも既に解ってしまったと思いますが、Divergence の定理の最終結果として、次の式が得られます。

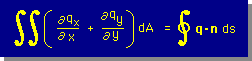
この式は、かなり重要ですので、ペンを持ったら自動的にこの式が書けるようになるまで、このDivergence の定理を勉強して下さい。なぜこの式がそんなに重要かと言うと、式の左と右とで、積分の次元が違うと言うことです。

Divergenceの定理の話しを、もーちょっと続けます。Divergenceとは、発散のことで、通常 divqで表わします。divqがプラスだと膨張、マイナスだと収縮の状態を示しています。divqの表示方法ですが、Index Notation で表わすと、下式の様になります。

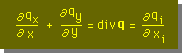
すると、Divergenceの定理は、次の2つの方法で表わすことが出来ます。

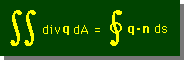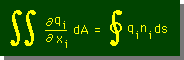これからも、このWeb上では、上の2つの表示方法をよく使いますので、しっかりと勉強しておいて下さい。