節点6と節点2間のHeat Flow は、要素1から要素2へ流れています。右手の法則で線積分するわけですから、その積分結果は、要素1の節点6-2間でプラスになり、要素2ではマイナスになります。つまり、q_nについて、次の事が言えます。

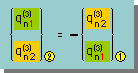
そして、前ページの積分を、Global 連立方程式にAssembleしたときに、下式の様な結果になります。

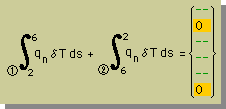
つまり、上式の右辺のベクトルの第2項目と第6項目がゼロになる。これにより、Inter-element Continuity を満足させたことになります。
全ての要素について、上と同様な計算をして、Assembly作業を行います。すると、領域内部の各節点では、境界積分項から計算される全ての値を合計すると、ゼロになっているはずです。
1次元でも、同様な結果になったことを覚えていますか。 参考のために見ておいて下さい。
したがって、境界積分項の計算が必要とされるのは、領域の境界を持っている要素のみになります。理解して頂けましたかな。つまり、領域内の要素間では、熱のやりとりのバランスが保証されていることになります。

■境界積分の項の計算が不要なケース■
境界積分項の計算方法について、4ページを費やしましたが、境界積分項の計算が不要なケースが有ります。下に2つのケースを示します。

• Dirichlet境界上　、出来上がった連立方程式に、Dirichlet境界条件をはめ込む時に、連立方程式の右辺をゼロにするためです。
• q_n = 0のNeumann境界上　境界積分項の計算がゼロになる。