■まとめ■
2次元有限要素法の説明では、これまでに、要素毎の領域積分と境界積分項の計算方法を紹介しました。ここでは、まとめとして、Global連立方程式について、簡単にふれておきます。詳細な計算手順については、次のExampleで紹介します。
まず、要素単位の積分式を下に示します。

WRMに従って、積分(I)を{δT}で微分してゼロとおきます。

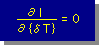
すると、要素単位の有限要素式が出来上がります。下がそうです。

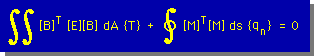
有限要素法では、連立方程式化するために、下のマトリックスとベクトルで上の有限要素式を表わします。下の式を見て下さい。

ここに、[sk]は、通称"Local stiffness matrix"と呼ばれ、3X3のマトリックスです、{Q}は、3つの値をもつベクトルです。

上式を全ての要素について計算し、1つの連立方程式にまとめると、次の様になります。

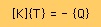ここに、[K]を通称"Global stiffness matrix"と言い、[K]の大きさは、節点数X節点数です。

上の式のままで連立方程式の計算をしても、未知数である温度(T)は計算されません。温度(T)を得るためには、Dirichlet境界条件を上の連立方程式に組み込む必要があります。やりかたは、1次元のときと、まったく同じです。実際の計算については、次のExampleを見て下さい。