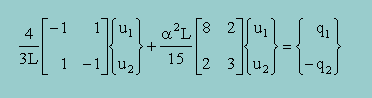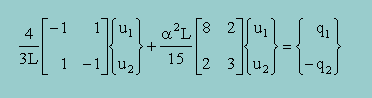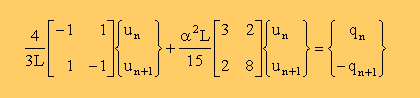One Dimensional Finite Element Method
Calculus of Variations-13
いつもの様に前のページの形状関数を使ってHelmholtz equation に重み付け残差法を適用します。
そしてNeumann B.C. が最初の要素にある場合は下のMatrix 式が得られます。
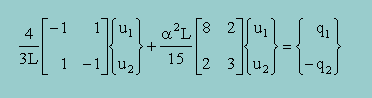 Neumann B.C. が最後の要素にある場合は下のMatrix 式が得られます。
違いはどこになるかと言うと[B]T[B]と[N]T[N]の両方の積分ですが特に
[N]T[N]に注目して下さい。
Neumann B.C. が最後の要素にある場合は下のMatrix 式が得られます。
違いはどこになるかと言うと[B]T[B]と[N]T[N]の両方の積分ですが特に
[N]T[N]に注目して下さい。
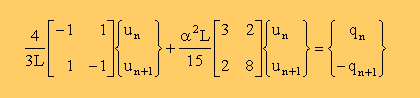 詳細はFortran プログラムのBUCKLE1C.FORを参考にして下さい。
計算に使った領域と境界条件は
以前紹介したものと同じです。
つまり最後の要素を上で紹介した形状関数で置き換えてあります。
そして要素分割数を2から10まで変化させてNeumann B.C. が設定してある節点でのu(x)を厳密解と比較してみました。
下図が計算結果です。
詳細はFortran プログラムのBUCKLE1C.FORを参考にして下さい。
計算に使った領域と境界条件は
以前紹介したものと同じです。
つまり最後の要素を上で紹介した形状関数で置き換えてあります。
そして要素分割数を2から10まで変化させてNeumann B.C. が設定してある節点でのu(x)を厳密解と比較してみました。
下図が計算結果です。
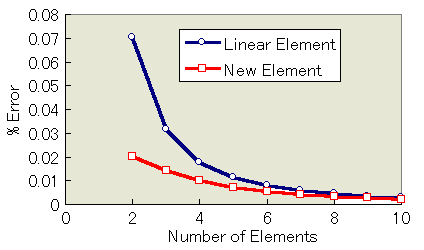 もともと線形要素で計算しても そんなに誤差が大きくありませんでしたので何とも言えませんが。
しかし 何らかの効果は有った様ですね。
境界付近を大きな要素で分割しても高い精度が得られていると言うことを上の図は言っています。
まー要素の次数が高くなっているので そのせいもあると思います。
もともと線形要素で計算しても そんなに誤差が大きくありませんでしたので何とも言えませんが。
しかし 何らかの効果は有った様ですね。
境界付近を大きな要素で分割しても高い精度が得られていると言うことを上の図は言っています。
まー要素の次数が高くなっているので そのせいもあると思います。
気を良くして2次要素でもプログラムを作成してみました。
が結果はNGでした。
この件については暇を見つけ次第 続きをやりたいと考えています。
これで変分法については終わりです。
理解できましたか。
有限要素法の本を見ても変分法をここまで噛み砕いて説明していません。
変分法には まだまだ先があります。
後は皆さんが勉強して下さい。
新しい発見をするかもしれませんよ。
変分法についてはDym and Shamesの本に まだまだ沢山載っています。
また読み易い本です。
なお変分法以外のところのページで積分式の値を表す記号として δI の代わりに I を使っています。
どっちにしろ I0 を基準にとるかゼロを基準にとるかの違いですから気にする必要はないでしょう。
また あまりギリシャ文字を沢山使い過ぎると頭が混乱するので δI の代わりに I を使って良かったと思っています。
皆さんはどう思いますかね。
次はまとめです。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method