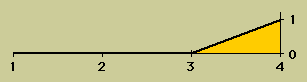 | Galerkin法 重み関数にN2=ξを使っている |
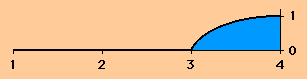 | 非Galerkin法 重み関数をN2(ξ)=ξ(2-ξ) で表している 節点4で微分がゼロになっている |
最初の条件は Galerkin method を使っていれば 自動的に満足します。 ところが 2番目の条件を満足させるためには重み関数(δy(x))を新たに作る必要があります。 重み関数を作る条件が1つ増えるので Galerkin method による重み関数よりも1つ次数が高くなります。
例えば 下図の上段に示す様に、線形要素で領域を3分割し Galerkin 法で重み関数を作ると dδy/dx は x=L でゼロになりませんよね。 ゼロにしろというのが 無理な話ですね。
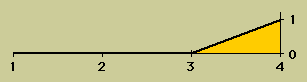 | Galerkin法 重み関数にN2=ξを使っている |
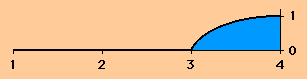 | 非Galerkin法 重み関数をN2(ξ)=ξ(2-ξ) で表している 節点4で微分がゼロになっている |
現時点では 2番目の条件を満足させた解析ソフトは無いと思います。 それでも解析は十分良い精度を出しているので2番目の条件は必要条件ではなさそうです。
上の図で非Galerkin法となっている理由は u(x)の近似に線形要素を使い、そして一番右の要素の重み関数に線形以外の関数を使っているからですよね。 早速、上の図にある形状関数で計算してみましょう。 まず形状関数は下表の様になります。貴方も確認してみて下さいね。
| 関数名 | Neumann B.C. が要素1 (上流)にある場合の式 |
Neumann B.C. が要素n (下流)にある場合の式 |
|---|---|---|
| N1 | 1-ξ2 | -2ξ+ξ2+1 |
| N2 | ξ2 | 2ξ-ξ2 |
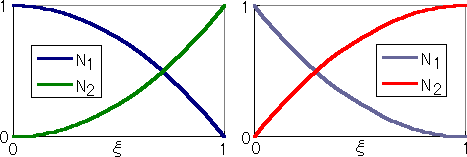
これらの形状関数を使ってプログラムを書いてみました。 まず 非Galerkin法で試してみましたが 精度の向上は みられませんでした。 そこで Neumann B.C.が設定される要素を上の形状関数で近似するGalerkin法でプログラムしてみました。 すると かなり良い結果が得られました。