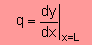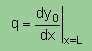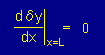One Dimensional Finite Element Method
Calculus of Variations-11

ところで Neumann Type の境界値ですが近似解(y(L))において x=L での値は下式で表していましたね。

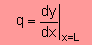では厳密解(y0(L))のNeumann Type の境界値はどうでしょう。 下式に示す通り近似解とまったく同じになります。

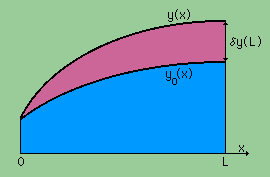
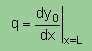すると近似解は、y(x)=y0(x)+δy(x) ですから重み関数(δy(x))の x=L での微分はゼロでなくてはなりません。

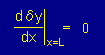これは ちょっと意外な条件です。 どっちにしろ これまでをまとめると次の様になります。

(1) δy(x) はNeumann type 境界でゼロにならない
(2) dδy(x)/dx はNeumann type 境界でゼロになる

上の2つの条件ですが wrm(重み付け残差法)で使いました。 この時点では近似式を作る条件として紹介しましたが、実は変分法から導かれている事実だったのです。

BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method