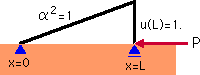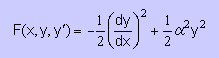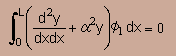
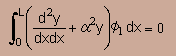
または
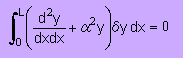
前にも言いましたが これが 重み付け残差法(WRM)の基本形です。 このことから言えることは重み付け残差法(WRM)は変分法の副産物だったと言うことが分かります。
ここまでで何か質問は有りますか と訪ねると多分 次の2つが上がると思います。
| (1)状態関数 は どうやって造るんですか |
| (2)δy(X)は どの様にして決めるんですか |
次の質問については なにも決まりはありません。 ただ、境界条件によって変分が存在するかどうかを考えるのみですね。 例えばDirichlet境界では、近似解=厳密解ですから変分は有りませんね。 ところがNeumann 境界では どうでしょうか。 これについては後で説明します。
■例題■
あまり理屈ばかりこねていては理解しずらいので何か計算してみましょう。
以前下図に示す状況を計算したことがありますので ここでもこの例題を取り上げることにします。
ここで α2=1、L=1、y(0)=0、y(L)=1 です。