■状態関数と微分方程式との架け橋■
では早速 Euler-Lagrange Equation の　F　に Helmholtz equation の　状態関数 を代入してみましょう。 まず 状態関数 を思い出してもらうために もう一度、表示します。

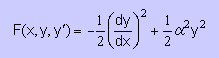
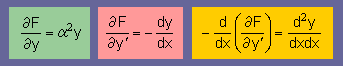
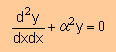
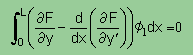<=====同じ=====>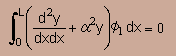

Euler-Lagrange Equation がこの世に現れたのが1760年ごろでした。 Lagrange が23才で Euler は52才でした。 有限要素法の歴史のところでも言いましたが Lagrange が Leonhard Euler(1707-1783)宛に手紙を書いたのが Euler-Lagrange Equation の始まりとなっています。

Jean Bernoulli(1667-1748) が変分法を始めたころ(1697)は問題をつくっては” どうだ おまえ解けるか”といった程度の学問でした。 それに比べると Euler-Lagrange Equation は 変分法の Breakthroughと言えます。

Euler-Lagrange Equation のお陰かどうかは分かりませんが変分法はその後も発展し Ritz method や弾性力学で有名な Castigliano の定理(最小仕事の原理)を生み出しています。 最近(1970年代)ではここで紹介している様に重み付け残差法(WRM)が変分法から考え出された結果、有限要素法が様々な分野で急速に使われ始めました。しかし 式の展開を見ると が先でEuler-Lagrange Equationが後のように思えます。なぜかと言うと境界要素法の式は重み付け残差法の形から始まっています。ただ重み関数がGreen関数になっています。

急速に発展した理由としてWRMが発見される以前の変分法では状態関数 の存在が不可欠でしたが 重み付け残差法(WRM)での解析では状態関数 が不要です。 また非線形の微分方程式でも解けるという方法だからです。