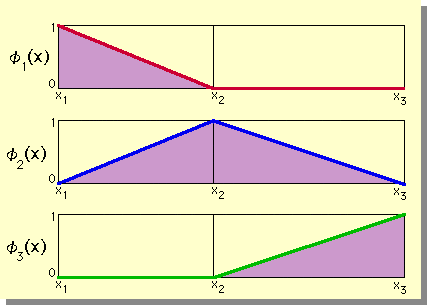
One Dimensional Finite Element Method
Linear Element-3

話を元に戻しましょう。さて、近似式は、どの様に書き表せばよいのでしょう。 また近似式に使われる関数はどの様な格好をしているのでしょう。 まず近似式は次の様になります。

u(x)= u(x1)φ1(x)+ u(x2)φ2(x)+ u(x3)φ3(x)

そして、上式の関数 φ1(x), φ2(x), φ3(x) の条件とて、 u(x1)=u1、u(x2)=u2、u(x3)=u3 を得るには下表を満足させなければなりません。 また、u1=u2=u3=1の場合を考慮すると、

φ1(x)+ φ2(x)+ φ3(x)=1

でなければなりません。これは要素にとって必要条件になっています。

関数 x1で x2で x3で
φ1 1 0 0
φ2 0 1 0
φ3 0 0 1

そして、近似式の中の関数 φ1(x)、 φ2(x)、 φ3(x) は下図に示す様な形になります。 座標x1からx2が要素１で座標x2からx3が要素2です。

これらは、かなり荒っぽい関数ですが近似式としての条件を満足しています。

■重み関数と未知数(u1, u2, u3)の管理区域■
重み関数としての条件も満たしています。 また、重み関数と密接な関係にあるのが未知数でしたね。 つまり ukの管理区域で重み関数φkは有限な値を持ちその区域外ではφk=0となるでしたよね。 したがって、上の図から ukの管理区域として ukが存在している要素と言うことになります。例えば、u1は、要素1に存在しています。 ですから、u1の管理区域は、x1からx2までとなります。 u2は、要素1と要素2に存在しています。管理区域は、x1からx3までとなります。

■境界条件■
φ1(x)と φ3(x)はDirichilet境界条件またはNeumann境界条件が与えられるように φ1(x1)=1と φ3(x3)=1になるように作れれています。 境界条件と境界値の挿入方法については例題のところで詳しく説明します。

BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method