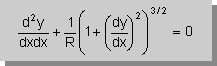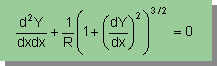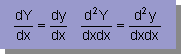One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-4
■円の式と円の微分方程式■
薄い鉄の板を3cmX30cm位の大きさに切断し、定規をつくります。
そして、定規の両端を溶接し、
下に示す様な真円をつくります。真円であるということは、
円のどの位置をみても、板の表面の張力応力と裏面の圧縮応力は、同じになるはずですよね。
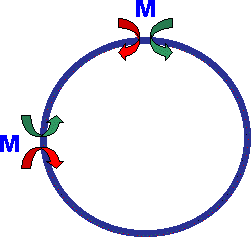 つまり、円上のどこでも、曲げモーメントの値は、同じということになります。
ここで問題にしているビームも両端に同じ曲げモーメントが作用しているので、
ビームが変形した状況は、円の一部であることが分かります。
つまり、円上のどこでも、曲げモーメントの値は、同じということになります。
ここで問題にしているビームも両端に同じ曲げモーメントが作用しているので、
ビームが変形した状況は、円の一部であることが分かります。
そこで、円の一部を表す微分方程式は、あるのか?です。
円の式は、知っていますよね。x2+y2=r2です。
では、この式を解とする微分方程式は、どんなかっこうをしているでしょう。次の様な式になっています。
つまり、ビームの微小区間において、yの2階微分、yの1階微分、1/Rとの関係を表して
いることになります。
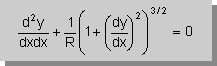
■曲率 1/Rは?■
ここで取り上げている定規で作ったビームには、両端にモーメントが作用していました。
このことは何を意味しているかと言うと、ビームは、半径Rの円弧を描き、
ビームの曲面は下の円の式で書けることになりますよね。
 そして、曲面では、下の円の微分方程式が成り立っていることになりますね。
そして、曲面では、下の円の微分方程式が成り立っていることになりますね。
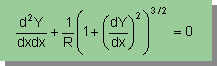 ここで注意してもらいたいことはy=Y+S ですから、
次の関係が成り立ちます。
何故かと言うと S は一定な値ですからね。
ここで注意してもらいたいことはy=Y+S ですから、
次の関係が成り立ちます。
何故かと言うと S は一定な値ですからね。
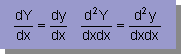 円の式が、円の微分方程式の解であるということを確認するために、次に示す関係式を、
円の微分方程式に代入してみて下さい。最も手っ取り早い方法として、
表計算法があります。
円の式が、円の微分方程式の解であるということを確認するために、次に示す関係式を、
円の微分方程式に代入してみて下さい。最も手っ取り早い方法として、
表計算法があります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method