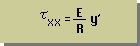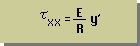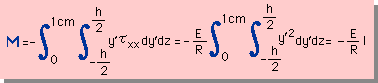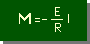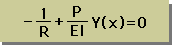One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-3
つまり、εxx=y'/R となり、εxx=τxx/E ですから、τxxは次の様に書けます。
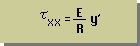応力τxxの分布は式から次のようになっています。
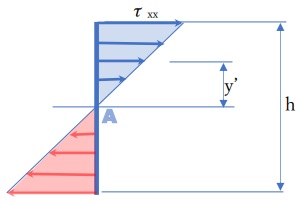確かに、応力分布は Linear になっていますね。もちろん、これは、τyy 存在を無視した結果ですけどね。
■Newtonの第2法則■
次に、微分方程式を導く前準備をします。技術的な問題を解決してくれる微分方程式は、次の法則から出来上がっています。
| 質量保存の法則 dm/dt+ΣQ=0 |
Newtonの第2法則 ΣF=dmv/dt |
エネルギー保存の法則 |
ここでは力の釣り合いが問題になっていますから、Newtonの第2法則をモーメントに適用した、
ΣMz=Iθdω/dt により微分方程式を導くことができます。
そして、ビーム全体は回転していないので、ΣMz=0 になります。詳しく書くと、次の様になります。
| ΣMz=(応力分布による断面でのモーメント)+(外力Pによるモーメント)=0 |
外力Pによるモーメントは、 Mp=rXF=Y(x)P です。下図を参考にして下さい。
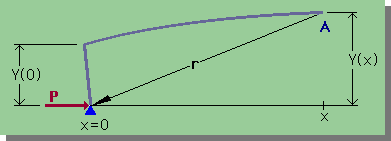
■応力分布による断面でのモーメント■
さて、次に必要なものは、Beamの応力分布による断面でのモーメントです。
モーメントは、アーム X 応力 X 面積であるから、次の様になります。
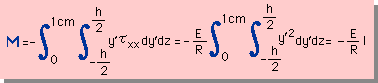結果から、断面でのモーメントは、Young Modulus(E)と断面2次モーメント(I)に比例し、半径(R)に反比例することになります。
つまり、下式の様になります。
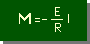よって、ΣMz=0 より、次の式が生まれます。
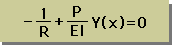
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method