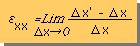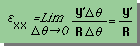One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-2
■応力分布は本当に線形か?■
応力分布については、Hooke's Law で調べることが出来ます。(Hooke's Law に関する事柄については、
Solid Mechanicsで詳しく紹介します。)
それは、
| εxx=(1/E){τxx-υ(τyy+τzz)} |
ここに、E=Young Modulus, υ=Poisson's ratio, εxx=x軸方向の歪(Strain), τij=i軸方向に直角な面に作用しているj方法の応力です。
もし、τyy=τzz=0 と仮定出来れば、εxx=(1/E)τxx と書けます。
多分、Cチャンネルの中央部分の1cmを考慮すれば、この仮定は、ほぼ正しい言えます。
”ちょっと待てよ、 τyy は、表面でゼロだけど、内部ではゼロになりません。
”と言いたい方があるかと思います。確かにそうですね。εyy が、ゼロじゃありませんからね。
多分、τyy は y軸方向に3次曲線を描くと思われます。
ちゃんとしたことはSolid Mechanicsで勉強するとして、
ここでは εxx=(1/E)τxx ということにしておきましょう。
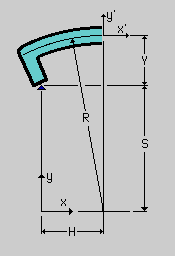
作業を始める前に、ここで使う座標を定義しておきます。
下の左の図を見て下さい。Beam の断面では、x'-y' を使います。
Beam の全体は x-Y 座標で表します。
そして 半径Rの円の中心は、(H,0) になります。
まず、Strainから始めましょう。
Strainは 力を負荷した後の伸び率を意味します。
式で表わすと次の左の様になります。
ここに、Δx=力を負荷する前の長さ、Δx'=力を負荷した後の長さを意味します。
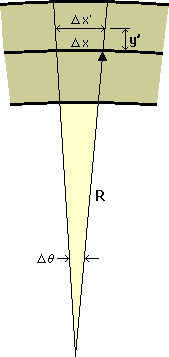
上の図は、ΔxとΔx'を極座標系(Polar Coordinates)で表わしています。
Rは、Beam曲率を表す半径です。
Δθは、原点からR行った点でΔxの幅になる角度です。
極座標では Δx=RΔθそしてΔx'=(R+y')Δθですから εxxは上の右の様になります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method