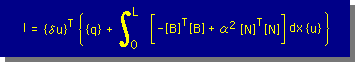
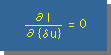
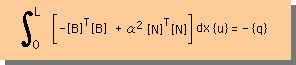
■Final Remark のまとめ■
Final Remark で勉強した事柄をまとめてみました。 新しい重み関数は、重み付け残差法のなかで最も重要な項目の1つです。 理解が深まるまで繰り返し勉強して下さいね。

Final Remark でのエッセンス

要素の近似式を定義する	u(x)=u1N1 + u2N2
新しい重み関数を定義する	δu(x)=δu1N1 + δu2N2
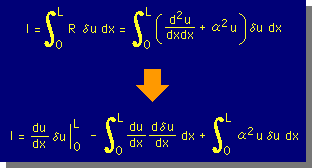
新しい重み関数を用い積分式を定義する
2階微分項に部分積分法を施す
Matrix表示法で積分式を書く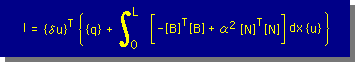
Iをδuiで微分しゼロと置くとMatrix型の要素の有限要素式が得られる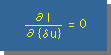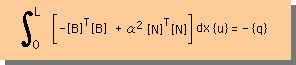
上式を積分する。 後は要素毎の積分の手順と同じです。
[B]T[B]の積分結果を[kij]で表すと右に示す特徴がある。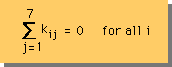
上の特徴を使うと [kij]の対角項は右の式で計算できる。
また、[kij]の行列値はゼロである。	Det[kij] = 0
[N]T[N]の積分結果を[geomij]で表すと右に示す特徴がある。