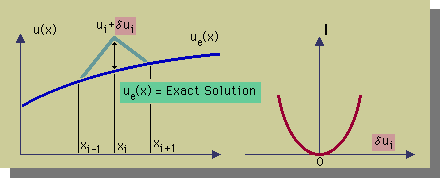
つまり I が最小になる点(∂I/∂δui=0) において I ＞ 0 であり δui＞ 0 でもある。 誤差が存在していることを意味しています。
次にもしu(x)が厳密解ue(x)だったらどうでしょう。 残差Rはゼロになります。では、下図の左に示すδuiをue(x)へ加算したらどうでしょう。 結果は下図の右になるのではないかと考えられます。 つまりδui=0の点では I=0 になります。■要素分割数を多くすると■
要素分割数を多くしたときの、I とδuiとの関係を考えてみましょう。
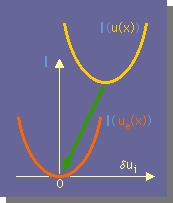
要素分割数が多くなると、I も小さくなり∂I/∂δui=0 が最小になるδuiも小さくなります。
要素分割数を更に多くすると解析結果は厳密解に近づき ∂I/∂δui=0になる点が下図のグラフの原点に近づくはずである。
次に進む前に左をクリックして問題を解いて下さい。
 | 内容について疑問および質問がある場合は左のQ&Aボタンを押して下さい。 |
|---|