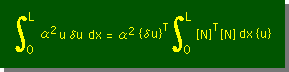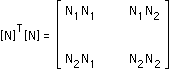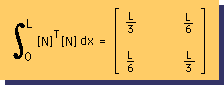One Dimensional Finite Element Method
Final Remark-6
■次に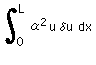 の項■
の項■
この項は通常 Source Term (生成項) と言われています。
そしてマトリックス表示を用いると{u}と{δu}は次の様になっていました。
| 近似式: | u(x)=[N]{u} |
|
重み関数: | δu(x)=[N]{δu} |
そして、前のページを参考すると生成項のマトリックス表示は次の様になります。
[B]が[N]に代わったと思えば良いでしょう。
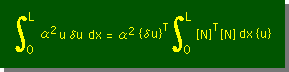 上の式中の[N]T[N]を前のページの[B]T[B]同様にマトリックス演算をすると次の様になります。
ここに[N]=[N1 N2]です。
またN1=1-x/L とN2=x/L であるということを頭に入れて[N]T[N]を0からLまで積分すると下図に示す様な結果が得られます。
上の式中の[N]T[N]を前のページの[B]T[B]同様にマトリックス演算をすると次の様になります。
ここに[N]=[N1 N2]です。
またN1=1-x/L とN2=x/L であるということを頭に入れて[N]T[N]を0からLまで積分すると下図に示す様な結果が得られます。
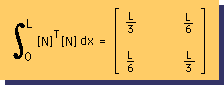 L/3やL/6はどこかで出てきましたよね。覚えていますか?。
ここでちょっと貴方に計算して貰いたいことがあります。
それは上のマトリックスの中味を全部足して貰いたいにです。
結果は L になりますね。
どうして L に成るか解りますか。
ちょっと考えてみて下さい。
L/3やL/6はどこかで出てきましたよね。覚えていますか?。
ここでちょっと貴方に計算して貰いたいことがあります。
それは上のマトリックスの中味を全部足して貰いたいにです。
結果は L になりますね。
どうして L に成るか解りますか。
ちょっと考えてみて下さい。
更に[B]T[B]同様に[N]T[N]も対称マトリックスになっています。
これも連立方程式の解法に有益な特徴です。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
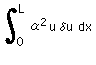 の項■
の項■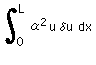 の項■
の項■