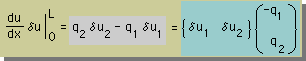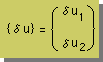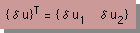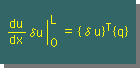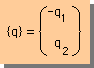One Dimensional Finite Element Method
Final Remark-3
■境界積分項■
前ページの積分式の境界積分項から観察してみましょう。
積分のルールに従って展開すると下の様になります。
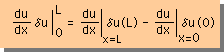 ここにδu(L)とδu(0)は次の様になるということを理解して下さいね。
解らなければ1次要素の形状関数
(N1 と N2)
をもう1度復習して下さい。
ここにδu(L)とδu(0)は次の様になるということを理解して下さいね。
解らなければ1次要素の形状関数
(N1 と N2)
をもう1度復習して下さい。
| δu(L) |
= |
N1(L)δu1+N2(L)δu2 |
| = |
0δu1+1δu2 |
| = |
δu2 |
| δu(0) |
= |
N1(0)δu1+N2(0)δu2 |
| = |
1δu1+0δu2 |
| = |
δu1 |
要素の境界では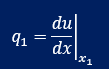 ですから境界積分項は次の様になります。
ですから境界積分項は次の様になります。
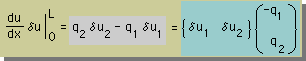 ベクトル形式の{δu}は下図に示す様に書けました。
ベクトル形式の{δu}は下図に示す様に書けました。
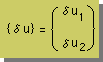 そしてMatrixで勉強したように{δu}のトランスポーズ(Transpose)は次の様になります。解らない人は復習して下さいね。
そしてMatrixで勉強したように{δu}のトランスポーズ(Transpose)は次の様になります。解らない人は復習して下さいね。
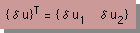 このページで学んだことを全て総合すると境界積分項はマトリックス表示を使うと次の様に簡単に書き表すことが出来ます。
このページで学んだことを全て総合すると境界積分項はマトリックス表示を使うと次の様に簡単に書き表すことが出来ます。
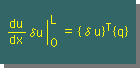 |
ここに、 |
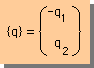 |
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
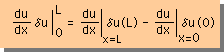
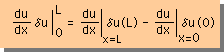
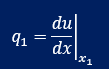 ですから境界積分項は次の様になります。
ですから境界積分項は次の様になります。