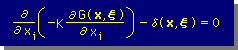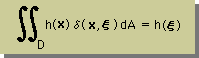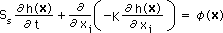前のセックションのFundamentalでは、境界要素法の概略を説明しました。 ここでは、境界要素法の基本式 ”境界要素式(Boundary Element Equation)”を Green's Identities からでなく、どんな微分方程式(全てではない)にも適応できるWeighted Residual Methodで導く方法を紹介します。

■Weighted Residual Method■
有限要素法で紹介した事柄を思い出して下さい。最初の2-3ステップは、有限要素法とまったく同じです。では、復習も含めて、Residualの定義から始めましょう。まず、微分方程式として下の2次元の地下水のConfined Flow を取り上げます。

上の式を定常にして、＝0 の形にすると、次の様になります。

微分方程式の h(x) に近似解を代入すると、上式はゼロにならず、Residualを生産することになります。このResidualに重み関数 G(x,ξ) を乗じて、その積に対し領域積分を施し強制的にゼロとします。以下の様になります。

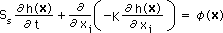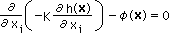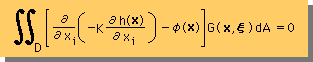
■Kernel function■
この重み関数は、有限要素法のそれと違い、下の微分方程式を無限領域で満足している関数が用いられます。その重み関数のことをKernel functionまたはfundamental solutionと言います。

上式のδ(x,ξ) は、2次元のDirac delta 関数で、点ξを除いて、δ(x,ξ)=0 になっています。また、点ξを含む領域では、下式の様な特性をもっています。