一定要素の最後のアップリケーションとして複数のゾーンを結合した領域(zoned non-homogeneous domain)の計算方法を紹介します。この方法が出来る様にになると、領域内の材料定数を場所ごとに変えることが可能になってきます。つまり、non-homogeneousのケースの計算が出来るようになるということです。いままでは、領域が1つでしたので、材料定数も1つでした。
■概要■
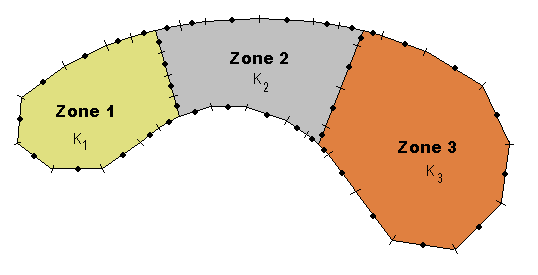
書物を調べると、下図に示す様にゾーン間をInterfaceと呼び、境界上と同様にポテンシャル値とその微分が定義されています。Heat equationの場合、温度と熱流速(heat flux)になります。下図に示す領域は、3つのZoneから構成されています。そして、それぞれのZoneに材料定数のK1、K2、K2が与えられています。境界条件は、これまでと同じDirichlet型とNeumann型で話を進めます。Zone間には有限要素法のInter-element-continuityでの条件と同じInterface条件を与えます。ここでは、これらの条件でLaplace Equationを解く方法を学びます。
| BACK to Straight | NEXT |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |