Two Dimensional Boundary Element Method
Multiple Domain Formulation-2
■境界要素式■
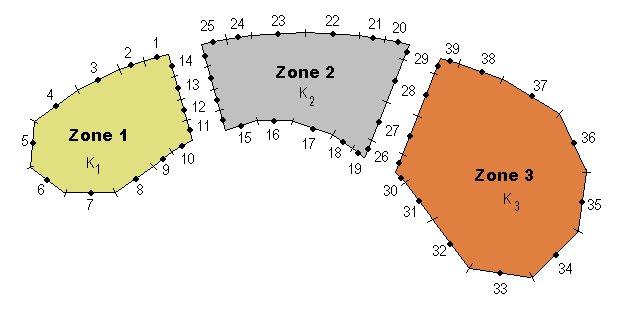
では、早速話をすすめることにしましょう。まず、下図を見て下さい。黒い点が要素を代表している節点でその近くに節点番号が書いてあります。Zone 1, 2, 3 の節点数は、それぞれ、14, 19, 14 になっています。Zone 1と 2間のInterfaceには、節点 11, 12, 13, 14 の４節点があります。Zone 2と 3間のInterfaceにも、節点 26, 27, 28, 29 の４節点があります。この様に、n個の一定要素を用いたゾーンを単位とした領域を考慮します。ゾーン内の要素数は、自由にに変えることが出来るようにしておきます。
まず、上図の各Zoneの境界とInterfaceを一定要素で分割した場合のマトリックス式を下に示しておきます。この式の導出は、前に詳しく説明してありますので、理解には問題ないと思います。問題ある方は、前に戻って復習しておいて下さい。
|
[C]{h}+[G]{qn}-[F]{h}={0}
|
上式を未知数毎にアレンジすると以下の様に書くことができます。
更に上式の両辺に-[G]-1を掛けると、以下が得られます。マトリックス[G]は、一定要素を使うと対称になります。マトリックス[F]は、残念ながら非対称になっています。
上式を有限要素法風にするために、[A]=-[G]-1[[C]-[F]]とすると、以下の様に書きます。
上のマトリックス[A]は、有限要素法のk[B]T[B]に匹敵します。違うのは、有限要素法の[A]が対称で、境界要素法が非対称になっています。このことは重要なポイントですので、しっかりと頭に入れておいて下さい。