ここでは、constant element を用い、最も簡単な領域を手計算で境界要素法のアルゴリズムを紹介します。その後、下の2つのプログラムを紹介します。

1つは、手計算と同じ手法の[C]{h}+[G]{qn}-[F]{h}={0} を生成する BEM8CON.FOR です。

もう1つは連立方程式 [A]{X}={RHS} を直接組み立てる BEM8CONQ.FOR です。プログラムBEM8CONQ.FORは、次のセックションのStraightで紹介します。この方法を用いると境界要素法に存在する角問題(corner problem)を緩和してくれます。

また、線形要素 (Linear element) と2次要素 (Parabolic element) については、Param のコーナーで紹介します。

■Steady Heat Transfer■
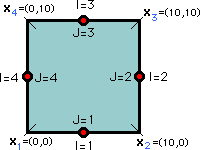
ここでは、シンプルな例題を紹介します。取り上げる問題は、定常の熱拡散です。つまり、Laplace equation を解くことになります。下の左の図を見て下さい。領域の左側と右側は断熱され、上面は100度Cに、下面は0度Cに保たれています。熱伝導係数は、K=1 とします。そして、 材料の境界を、下の右の図に示す様に4つのconstant element(一定要素) で分割します。文字 J＝ は、要素番号を、そして文字 I＝ は Source point の番号を意味します。そして、xの添え字は、要素の端点の番号です。

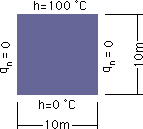前にも言いましたが、h(ξ) と q_n(ξ) は、要素中央の節点で計算されます。詳しくは、一定要素の説明のところを復習して下さい。

上の例題ですが、厳密解は、下図の様になります。つまり、温度分布h(x,y)は線形になり、q_nのHeat flux は上下で一定でサイドはゼロになります。手計算で簡単に計算できますね。

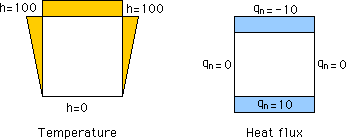
ここで注目して頂きたいのがq_nです。温度のh(ξ)と違ってq_nは、角で不連続になっています。つまり、境界要素法は、この不連続性に直面することになるのです。これをなんとかしないと設計の道具として成り立ちません。この不連続性を corner problems と呼んでいます。