つまり、境界上のどの要素でも、h(x) かまたは∂h(x)/∂n が指定されていることになります。逆に、h(x) かまたは∂h(x)/∂n が未知になっていることになります。したがって、境界上に、 数 n の節点があると、数 n の未知数が存在することになります。下図では、境界を12本の連結した直線で近似しています。節点数も12です。

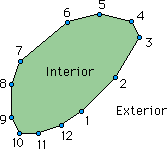
数値計算を行える様にするためには、source point ξ を境界上の節点番号1に置き、下の境界積分式に従い、数値積分を行います。

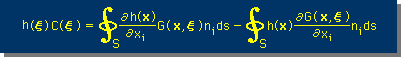
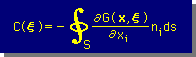
計算を行うと、 n 個の h(x)と n 個の∂h(x)/∂n を含む1行の線形代数式が出来上がります。この計算を全ての節点で行うと、n行の線形代数式が出来上がることになります。そして、 n 個の h(x)と n 個の∂h(x)/∂nの半分は、既知ですから、未知数は、n になります。つまり、未知のh(x) と∂h(x)/∂n が求まることになります。

このように、境界要素法は、境界上の節点のみで微分方程式を解く方法です。つまり、有限要素法と違って、領域内には、未知(unknowns)の変数を計算をするための節点は設けません。

次のセックションでは、与えられた微分方程式から、境界要素式を導く手順を紹介します。