ここに、θは、内角を意味することになります。スムーズまたは直線の境界上に点ξがあると、θ=π ですから、C(ξ)=1/2 になります。内角θのサンプルを下図に示します。
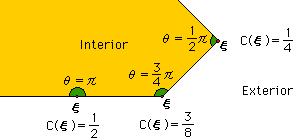
最後に、Source point が領域外にある場合を考えてみましょう。結果は、C(ξ)=0 になります。理由は、積分範囲が、特異点であるSource point を含まないからです。
これまでの3つのケースをまとめると、下表の様になります。
| ξの位置 | C(ξ)の値 |
|---|---|
| 領域内 | 1 |
| 境界上 | 内角/(2π) |
| 領域外 | 0 |
境界要素法の書物を読むと、この積分について、納得しがたい説明がなされています。それは、”ξ点が境界上に有る場合、ξ点の近傍では、∂G/∂r の特異性が強く数値積分が出来ない(improper integral)” と書いてあります。これは、大きな誤解です。後程、この点について詳しく説明します。
■Fundamental Solution の意味■
ここまでを復習すると、Fundamental Solutionには、ある特徴があることがわかります。つまり、Fundamental Solutionは、以下の微分方程式を満足する解ということです。
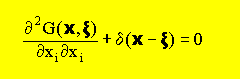
Source point(ξ)を含まない場合、Laplace Equationを満足していることになります。上式のδ(x-ξ)は、デルタ関数と言ってδ(0)でプラス無限大になり、それを積分すると1になります。実際は、上の式を満足するFundamental Solutionを見つけることからBEMの作業が始まります。 例えば、定常のheat equationを解くことを考えます。そして無限領域内のx=ξの位置に値が1の仮想熱流量(δe=1)を投入します。すると温度分布は、δh(x)=G(x,ξ)δeになります。この(δe=1がデルタ関数を積分した値になります。温度分布(δh(x))が有限要素法で言う重み関数と同じになります。境界要素法でも以下の式がスタートポイントになります。
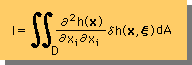
有限要素法で学んだ様に、マトリックス式が出来た時点で、∂I/∂δe=0とすれば、連立方程式が出来上がります。後で紹介する弾性解析では、仮想変位をδhi(x)=Gij(x,ξ)δej で表すことになります。なぜかと言うと、変位はベクトルであるため、仮想力のδejもベクトルになり仮想変位から簡単にオミットできないからです。しかし、熱解析の仮想温度(δh)や地下水解析の仮想水頭(δh)の場合、仮想熱流量はδe=1のスカラーですから、δh(x)をG(x,ξ)で置き換えることが出来ます。したがって、以下の説明も当分の間δh(x)でなく、G(x,ξ)で話を進めることにします。
■数値計算への応用■
これまでは、Green が残してくれた産物を紹介してきました。これからは、この産物をどのように数値計算へ応用できるかの概要を説明します。詳細については、後程、例題を交えて紹介します。
まず、Laplace equation の境界条件ですが、以下の2つが有ります。
| h(x) | と | ∂h(x)/∂n |
ここに、∂h(x)/∂n = ∂h(x)/∂xini です。
| BACK | NEXT |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |