Electromagnetics and Ham Radio
Offcenterfeddp 06
■ベクトルポテンシャルA(ξ)の計算とアンテナに流れる電流■
書物などによるとアンテナの線が細い場合、電流分布はcosineまたはsineで表しても問題なさそうとあります。書物などでは、以下の２式で電流分布を近似しています。
|
\begin{eqnarray}
I\left(z\right)=I_0cos\left(kz\right)
\end{eqnarray}
|
または
|
\begin{eqnarray}
I\left(z\right)=I_0sin\left(k\left(h-\left|z\right|\right)\right)
\end{eqnarray}
|
ただし、上の2式は、λ/4≧z≧-λ/4の範囲でのみ有効です。そしてアンテナの両端でゼロになっていなければなりません。
ここに、
|
\begin{eqnarray}
k=\omega\sqrt{\varepsilon\mu}=\frac{2\pi}{\lambda}
\end{eqnarray}
|
電流I(z)は、アンテナの断面を流れる分布電流ではなく、分布電流×断面積というふうに考えます。
つまり、電流は線の中心に集中して流れているものと仮定します。
ですので、Azの積分式はz軸方向の一次元になります。
そしてSource point(x)とObservation point(ξ)
は、z軸方向のアンテナ断面の中心線上に置きます。
つまり、電流Jをアンテナ導線(半径=a)の中心に質点化すると、電流は下式で示すI(z)で置き換えられます。
|
\begin{eqnarray}
I\left(z\right)=\int_{0}^{2\pi}\int_{0}^{a}{\mathbf{J}dr^\prime r^\prime d\theta}
\end{eqnarray}
|
結果的に、ベクトルポテンシャルAz(ξ)は以下の様になります。
積分リミットのhはλ/4です。
|
\begin{eqnarray}
A_z(\xi)=\frac{\mu}{4\pi}\int_{-h}^{+h}{I(z)\frac{exp\left(-jkr\right)}{r}dz}
\end{eqnarray}
|
ここで注意したいのが、座標zがSource point(z)でξがObservation point(ξ)です。つまりr=|z-ξ|です。
Green関数を使うとここら辺の考えが混乱してきますのでしっかりと確認しておいてください。
まず、インダクタンスとキャパシタンスと同じように、上式のAz(ξ)を計算しておきます。
積分にGauss-Legendre法を使っています。ここでの注意点は、r=0にならないようにしなければなりません。
偶数のサンプリング点のGauss-Legendre法だと微小積分セグメントの始点、終点、中央点を使いませんのでr=0になる心配はありません。
奇数のサンプリング点だと微小積分セグメントの中央点を使いますのでr=0になってしまいます。
下図は、ダイポールアンテナの左のエレメントを4セグメントに分割した状態を示します。
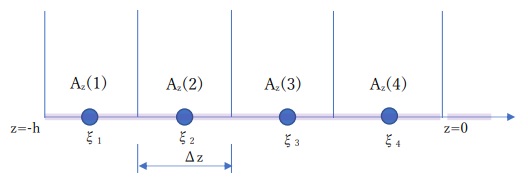
各々のセグメントで上式の積分を計算します。ここではObservation point(ξ)として図の青●の位置にしました。
ξ1でAz(ξ)を計算する場合、ξ=ξ1として上の積分を実行します。
全てのObservation point(ξ)でAz(ξ)を計算します。
各々のセグメントの長さはΔzで青●はΔzの中心にあります。ということは、Gauss-Legendreで積分の際、r=0にならないために、上でも言いましたが、偶数のサンプリング点数を選ぶ必要が有ります。
次の話題を説明しやすくするために計算されたAz(ξi)をAz(I)とよびことにします。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off-Center-fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO