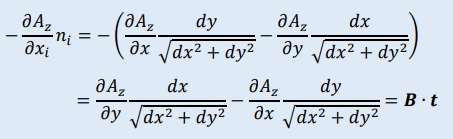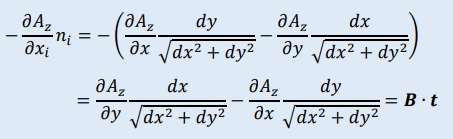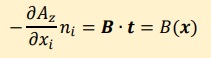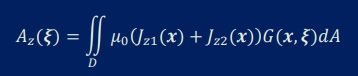Electromagnetics and Ham Radio
Inductance8
B(x)とAz(x)の関係ですが、境界要素法で-▽2Azに部分積分を施す過程があります。
以下のような結果になります。
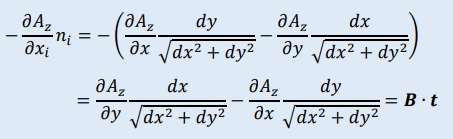 Ampere's Lawの説明で紹介したように、
ここでは導線の表面においてB・tをB(x)と記述しています。
また上式の、niは、単位ノーマルベクトル>nのnxかnyです。
要約すると、以下の様になります。
Ampere's Lawの説明で紹介したように、
ここでは導線の表面においてB・tをB(x)と記述しています。
また上式の、niは、単位ノーマルベクトル>nのnxかnyです。
要約すると、以下の様になります。
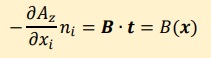 境界要素法で微分方程式を展開する利点の1つとしと、境界条件が明確になることです。
ですから、境界要素法による積分式の境界積分項を見ると、境界条件としてB(x)とAz(x)が考えられます。
境界要素法で微分方程式を展開する利点の1つとしと、境界条件が明確になることです。
ですから、境界要素法による積分式の境界積分項を見ると、境界条件としてB(x)とAz(x)が考えられます。
 そして計算しなければならない式は、以下でした。
そして計算しなければならない式は、以下でした。
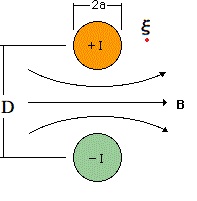
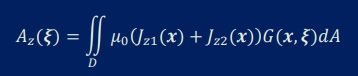 両導線の断面に対して上式の領域積分を行います。
磁気ベクトルポテンシャルAzの値を計算したい点ξは、領域積分の内外どこでも置くことが出来ます。
両導線の断面に対して上式の領域積分を行います。
磁気ベクトルポテンシャルAzの値を計算したい点ξは、領域積分の内外どこでも置くことが出来ます。
数値的に領域積分を行うには、導線の断面を要素分割する必要があります。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO