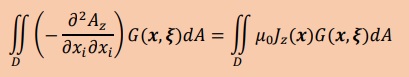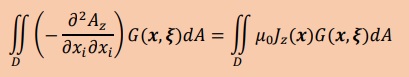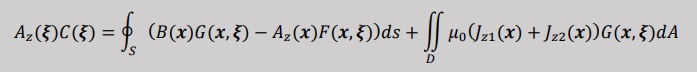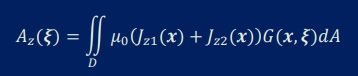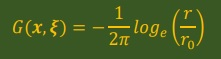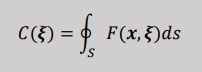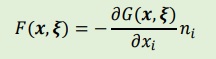Electromagnetics and Ham Radio
Inductance7
そしてG(x,ξ)を上式にかけ領域積分します。下式のようになります。
カーネル関数のことをGreen's Functionとも言います。
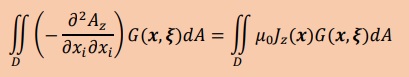 上式を境界要素法のルールに従い部分積分2回施すと、以下の境界要素法のよる積分式が得られます。
上式を境界要素法のルールに従い部分積分2回施すと、以下の境界要素法のよる積分式が得られます。
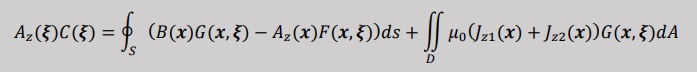 上式のC(ξ)は、計算領域が全て領域内ですので、C(ξ)=1になります。
詳細は、境界要素法(BEM)でチェックしてください。
上式のC(ξ)は、計算領域が全て領域内ですので、C(ξ)=1になります。
詳細は、境界要素法(BEM)でチェックしてください。
■境界条件について■
境界要素法で微分方程式を展開すると、境界条件が浮き彫りになります。
上の式の境界積分の項を見て下さい。
B(x)とAz(x)が未知数になっています。
境界要素法では、上式の境界積分を境界要素で近似します。
そして各々の境界要素において、B(x)またはAz(x)の
いずれかに値を与えなければなりません。つまり、どちらかが既知になっていなければなりません。
例えば、Ampere’s LawでB(x)を計算し境界条件として与えることが出来ます。
また、ベクトルポテンシャルが逆対称になっている面に(又は線に)Az(x)=0を与え、
計算領域を半分にすることが出来ます。B(x)を与える境界条件のことをNeumann型と言い、
Az(x)を与えることをDirichlet型と言います。
■ペア導線の場合■
今回の問題において、電流の+1[A]と-1[A]を適用させるので(doubletになっている)、無限遠点では、磁束はゼロになります。
したがって、磁気ベクトルポテンシャルAzもゼロになります。ということは、
今回の問題に限って上式の境界積分は、消えることになり、以下が残ります。
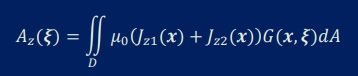 ここに、ラプラス方程式のカーネル関数は、以下になっています。式中のξは、
Azの値を計算してほしい座標を意味します。
そして、xは、電流Jzが流れる導線を要素で分割している座標を示します。
ここに、ラプラス方程式のカーネル関数は、以下になっています。式中のξは、
Azの値を計算してほしい座標を意味します。
そして、xは、電流Jzが流れる導線を要素で分割している座標を示します。
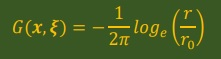 式中のr0は、基準の長さで値は1だと思ってかまいません。その他、式に現れている関数は以下で計算します。
詳細については境界要素法(BEM)のページを参照してください。
式中のr0は、基準の長さで値は1だと思ってかまいません。その他、式に現れている関数は以下で計算します。
詳細については境界要素法(BEM)のページを参照してください。
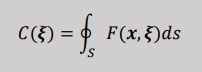
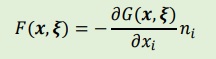
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO