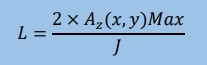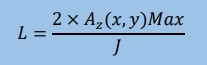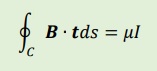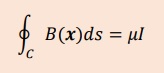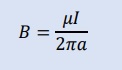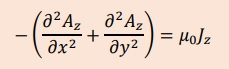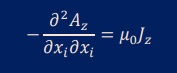Electromagnetics and Ham Radio
Inductance6
ここでは、最小のAz(x,y)=-最大のAz(x,y)になっているため、自己インダクタンス(L)は、次の様に書けます。
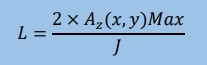 先へ進む前に、Ampere's Lawについて触れておきます。これは、本解析のノイマン型(Neumann type)の境界条件になります。
電流Iが流れる半径aの導線を取り巻く閉ループCの円周上では、以下の関係が有ります。
先へ進む前に、Ampere's Lawについて触れておきます。これは、本解析のノイマン型(Neumann type)の境界条件になります。
電流Iが流れる半径aの導線を取り巻く閉ループCの円周上では、以下の関係が有ります。
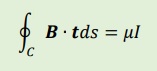 式中のB・tはベクトルの内積ですから、
下式のようにスカラーB(s)またはB(x)と書けます。B(s)の座標sは、導線表面の円周方向の距離を示します。
式中のB・tはベクトルの内積ですから、
下式のようにスカラーB(s)またはB(x)と書けます。B(s)の座標sは、導線表面の円周方向の距離を示します。
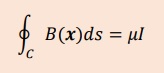 B・tが円周上で一定だと仮定できれば、
B(s)はBと書け、書物でよく見かける以下の式になります。
B・tが円周上で一定だと仮定できれば、
B(s)はBと書け、書物でよく見かける以下の式になります。
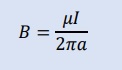 のちほど上式を使った境界要素法の計算を紹介します。
のちほど上式を使った境界要素法の計算を紹介します。
■境界要素法で解く場合■
境界要素法の特徴は、無限領域が扱えることです。
流体力学や弾性力学では有限域に境界があるので、有限要素法を使うことが多いです。
もちろん、境界要素法も有限域境界の問題を解く方法として設計現場で使われているのは言うまでもありません。
今回解く微分方程式は、下のポアソン方程式です。
境界要素法で紹介している式の展開に合わせるため、以前の式の両側に-1をかけてあります。
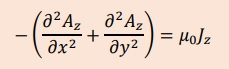 上式の展開では、よくインデックスノーテーション(Index notation)を使います。
すると、次のように短く記述でき、今後の式の展開にこれを使います。
インデックスが1つの項に2つ出現すると繰り返しを意味します。
上式の展開では、よくインデックスノーテーション(Index notation)を使います。
すると、次のように短く記述でき、今後の式の展開にこれを使います。
インデックスが1つの項に2つ出現すると繰り返しを意味します。
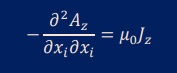 上の式は、-▽2Az=μ0Jzとも書くことも多々あります。
このような問題には、ラプラス方程式のカーネル関数を使います。
ただし、上式の右辺に対し領域積分を行う事が必要になってきます。
境界要素法では、ラプラス方程式のカーネル関数G(x,ξ)を準備する必要があります。
上の式は、-▽2Az=μ0Jzとも書くことも多々あります。
このような問題には、ラプラス方程式のカーネル関数を使います。
ただし、上式の右辺に対し領域積分を行う事が必要になってきます。
境界要素法では、ラプラス方程式のカーネル関数G(x,ξ)を準備する必要があります。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO