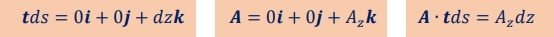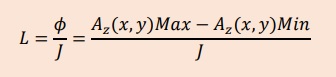Electromagnetics and Ham Radio
Inductance5
下図を見て下さい。ペア導線に+1[A]と-1[A]の電流が流れています。
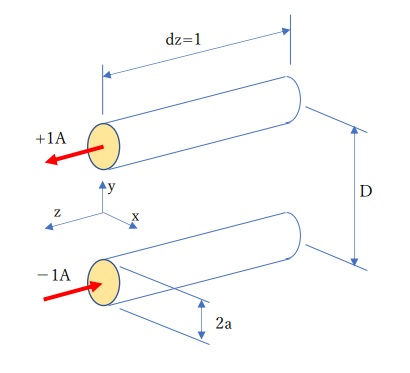 導線の半径はa、2つ導線の中心間の距離はDです。磁束は、導線の間に右ねじの法則に従い発生します。
つまり、右手の親指が電流の向きで、残りの4本の指の向きが磁束方向になります。
このような条件においてA・tの線積分の線Cは、
ペア導線から発生する磁束を全て捕まえるような閉ループでなければなりません。
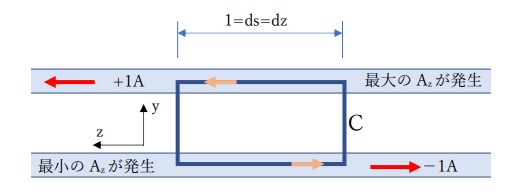
つまり、下図のようなループが考えられます。
導線の半径はa、2つ導線の中心間の距離はDです。磁束は、導線の間に右ねじの法則に従い発生します。
つまり、右手の親指が電流の向きで、残りの4本の指の向きが磁束方向になります。
このような条件においてA・tの線積分の線Cは、
ペア導線から発生する磁束を全て捕まえるような閉ループでなければなりません。
つまり、下図のようなループが考えられます。
 すると、積分オペレーター(tds)は簡略化されます。つまり、下に示す様な結果になります。
すると、積分オペレーター(tds)は簡略化されます。つまり、下に示す様な結果になります。
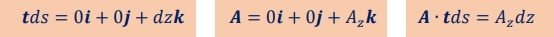 上図のループCがz軸と並行になったとき積分すればよいのです。
したがって、2次元空間での磁束Φは、下式で計算できる。
上図のループCがz軸と並行になったとき積分すればよいのです。
したがって、2次元空間での磁束Φは、下式で計算できる。
Φ=(最大のAz)×dz - (最小のAz)×(-dz)
磁界の分布は、上図の場合上下対称になっているので、最小のAzは、負の最大のAzになります。
ですから、
Φ=2×(最大のAz)
となります。
■2次元空間での自己インダクタンスの計算方法■
線状の閉回路での自己インダクタンスは、これまでに説明してきた方法で計算できますが、
線間の距離が線の直径とオーダー的に同等の値を有する場合は、線間を通過する磁束の決定には、
上で説明したように多少の技術的な配慮が必要になります。
まず、自己インダクタンスは、ペア導線が生みだす最大の磁束Φをその電流で割れば計算できます。
つまり、ペア導線に流れる電流をJとすると、 自己インダクタンスLは、下式で得られる。
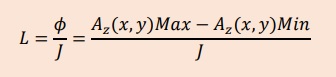 集中電流のスカラー記号にJとIを使っています。ベクトルJから由来しているときと集中電流のときはJ、法則や定義の説明の
その他の集中電流のときにはIを使っています。また、Jz(x)と記している場合は、分布電流を意味します。
集中電流のスカラー記号にJとIを使っています。ベクトルJから由来しているときと集中電流のときはJ、法則や定義の説明の
その他の集中電流のときにはIを使っています。また、Jz(x)と記している場合は、分布電流を意味します。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO