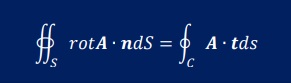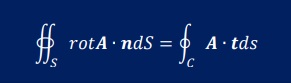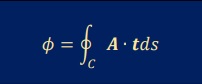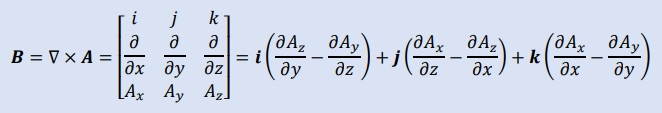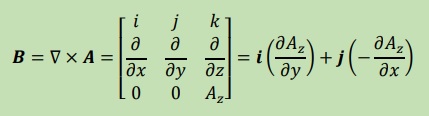Electromagnetics and Ham Radio
Inductance4
回転についてはストークスの定理を使うと、閉ループCのつくる面の積分を閉ループCの線積分で表すことができます。
つまり、下式です。
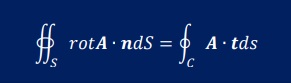 よって、磁束Φは、上図の閉ループC上の磁気ベクトルポテンシャルAを線積分することで得られることになります。
よって、磁束Φは、上図の閉ループC上の磁気ベクトルポテンシャルAを線積分することで得られることになります。
つまり、下式である。
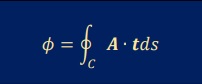
閉ループCをJzの電流により発生する全ての磁束Φを捕まえられるように設定すればよいことになります。
■2次元空間での磁束の計算方法■
ここでは、ペア導線の周りに発生する磁束Φを計算したいので、
下図に示すx-y 平面内の磁束密度(B)のみを考えます。
すると、復習になりますが磁気ベクトルポテンシャルAのx軸とy軸方向の成分は、ゼロになります。
これは下式のB=rotA=▽×Aから明白です。
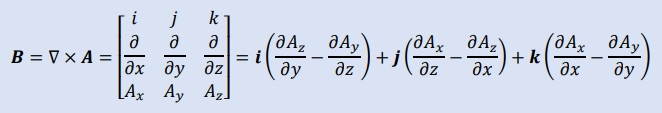 磁束密度(B)については、x-y面のみに対象であるのみで、z軸方向の成分は関係ありません。
更にz軸方向の微分も関係ないので、x-y面の2次元では、以下になります。
磁束密度(B)については、x-y面のみに対象であるのみで、z軸方向の成分は関係ありません。
更にz軸方向の微分も関係ないので、x-y面の2次元では、以下になります。
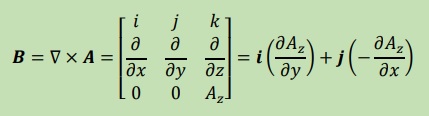 つまり、微分方程式▽2Az=-μ0Jzを電流Jzと適切な境界条件でAzを解けばBが計算でき、
更にA・tの線積分から磁束が得られ、結果、磁束を電流Jzで割れば自己インダクタンスが計算できます。
実感が湧かないので、もっと実際的な例題で上述の計算方法を説明します。
つまり、微分方程式▽2Az=-μ0Jzを電流Jzと適切な境界条件でAzを解けばBが計算でき、
更にA・tの線積分から磁束が得られ、結果、磁束を電流Jzで割れば自己インダクタンスが計算できます。
実感が湧かないので、もっと実際的な例題で上述の計算方法を説明します。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO