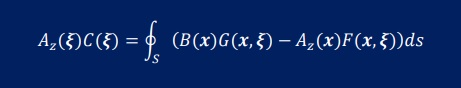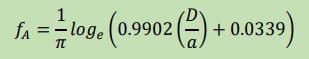
上の図から分かるように、点Aの計算結果( Domain IntegralΦA)の近似関数fAとf1の結果がほぼ同じになっています。 電流を導線の中心に集中させた場合と電流を等分布にした場合、点Aでは同じ磁束になるということです。 また、書物等では関数f1が使える条件としてD>>aとなっていますが、何と比較してこの条件が出てきたのでしょうか。 Domain Integral ΦBはB点での磁束です。下のfBが近似式です。関数f7とほぼ同じです。
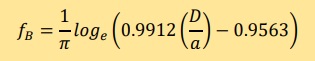
その他、f1, f2, f3は書物等で見る近似式で、f1とf2は既に上で紹介してあります。 そして、 f3は以下の様になっています。
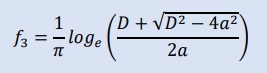
この関数 f3は、どのようにして導かれたのか今のところ不明です。 上の図から判断して点Bから点Aの円周上にあり、位置はD/aの関数になっているようです。 つまりD/a=2近傍では点B 付近に、D>>aでは点A近くに観測点ξが有るようです。 また、 f3は以下の様書けます。この様に書くとD/a=2で f3=0になるのがわかります。
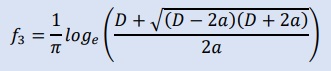
結果を見るとAzの最大値-最小値の線(Domain Integral Φmax)の数値が一番高く出ています。 点Bの計算結果(Domain Integral ΦB)が最小の値になっています。また、 今回取り上げているペア導線ですが、D/a=2で2つの導線は、接触します。 ただし、導線の断面は円ですから、面接触でなく線接触になります。 面で接触していないのでショートはしていないことになります。 また、本例題での計算結果から判断して点Bの計算結果を除いてはD/a=2で以下が言えそうです。
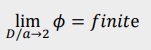
■例題2-1: B(x)を境界条件としてAzを計算する方法■
今度は、導線に電流を与えるのでなく、
それ相当の磁束密度B(x)をAmpere's Lawにしたがって、
導線の周りに一定の値を与えたらどうなるか計算してみます。
上の計算結果から導線の表面の磁束密度は、一定でないことが分かっていますので、
ここでの計算手法は近似解ということになります。
まず、計算式ですが、以下になります。
導線の表面に磁束密度を境界条件として与えるので導線内の領域積分は不要になります。
といより、導線部分の面積は、計算領域外になります。