Electromagnetics and Ham Radio
Inductance11
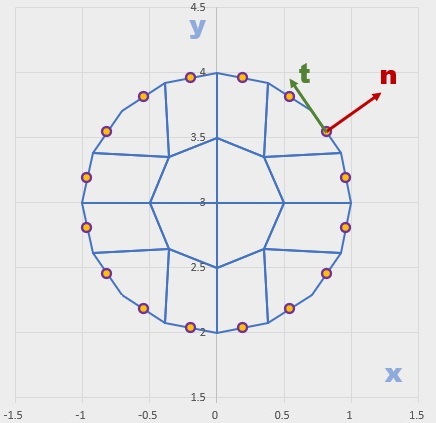 ベクトルポテンシャルAzのn方向の微分は、差分を使いました。計算結果は、
DPDN.SOL
に書き込まれています。
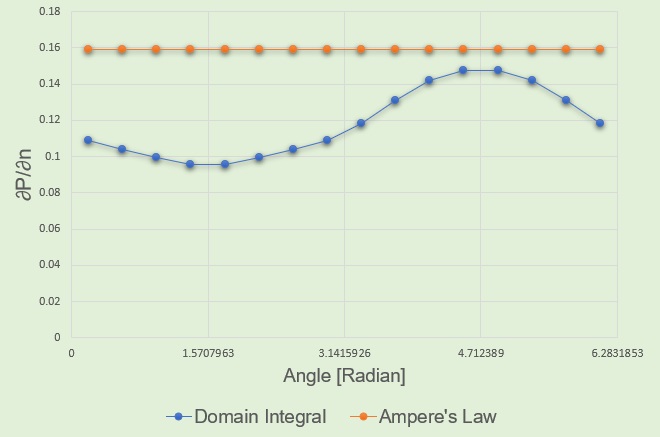
それをエクセルでプロットすると下図(左側)になります。
橙色の線がAmpere's Lawによる値(B=I/(2πR)=0.159)で、青色の線が今回の境界要素法での結果です。
導線の下側つまり、ペアのもう1つの導線に近い側(πから2π)ではAmpere’s Lawの値に近いですが、
導線の上側(0~π)ではAmpere's Lawの値より低くなっています(π=3.14159のパイです)。
矛盾の無い結果と考えてよいと思います。
ベクトルポテンシャルAzのn方向の微分は、差分を使いました。計算結果は、
DPDN.SOL
に書き込まれています。
それをエクセルでプロットすると下図(左側)になります。
橙色の線がAmpere's Lawによる値(B=I/(2πR)=0.159)で、青色の線が今回の境界要素法での結果です。
導線の下側つまり、ペアのもう1つの導線に近い側(πから2π)ではAmpere’s Lawの値に近いですが、
導線の上側(0~π)ではAmpere's Lawの値より低くなっています(π=3.14159のパイです)。
矛盾の無い結果と考えてよいと思います。
しかし計算結果に対し逆にAmpere's Lawで電流を計算すると、I=0.789でした。
これは、電流を導線の断面に等分布で与えた結果と考えられます。
そこで、導線の中心からR=2の円周上で磁束密度を計算してみました。以下(右側の図)がその結果です。
Ampere's Lawによる磁束密度は、B=I/(2πR)ですからB=0.0796になります。
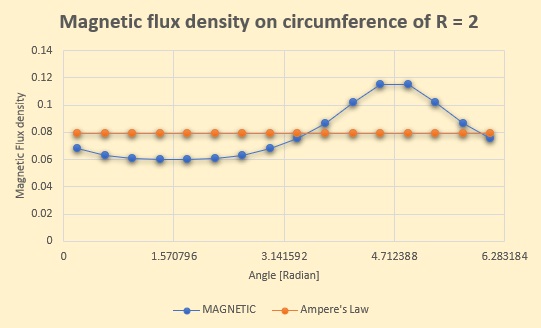 境界要素法での計算結果に対してAmpere's Lawで電流を計算すると、I=0.993が得られました。
ほぼ与えた値のI=1ですので境界要素法の積分は正常に行われていると考えてよいと思います。
境界要素法での計算結果に対してAmpere's Lawで電流を計算すると、I=0.993が得られました。
ほぼ与えた値のI=1ですので境界要素法の積分は正常に行われていると考えてよいと思います。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO



