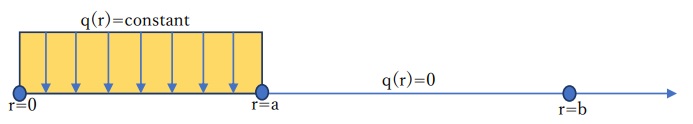Electromagnetics and Ham Radio
Coaxial8
全ての要素に対し、上式を計算しアッセンブルすると、節点数×節点数の連立方程式が出来上がります。
そしてr=0又はr=aに適切なNeumann条件をそしてr=bの編組線の電位V=0のDirichlet境界条件を与え
連立方程式を解くと全ての節点での電位が得られます。詳細については有限要素法のページ
Integral By Element
Final Remark
を参考にして下さい。
■1次元の分布電荷q(r)の単位と値■
ところで、分布電荷qの単位ですが2次元の場合[C]/[L2]のq(x,y)=Q/(πa2)ですが、
1次元の場合単位は[C]/[L]でなければなりません(π=3.14159....のパイです)。
Qは導線の中心での集中電荷で単位は[C]です。
まずここで取り上げた軸対称の微分方程式を見て下さい。
下に再度表示しておきました。
|
\begin{eqnarray}
-\frac{d}{dr}\left(r\frac{dV}{dr}\right)=\frac{q(r)}{\varepsilon}
\end{eqnarray}
|
分布電荷q(r)は、下図に示す様に半径rが0からaまでの間一定とします。
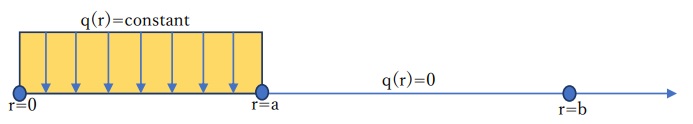すると、微分方程式のdV/drも一定である必要が有ります。
微分方程式の左辺は、微分のルールから以下になります。
dV/drが一定であるということに注目してください。
|
\begin{eqnarray}
\frac{d}{dr}\left(r\frac{dV}{dr}\right)=\frac{dV}{dr}\frac{d}{dr}\left(r\right)+r\frac{d}{dr}\left(\frac{dV}{dr}\right)=\frac{dV}{dr}
\end{eqnarray}
|
したがって、微分方程式が満足するには、以下のようになっていなければなりません。
|
\begin{eqnarray}
-\frac{dV}{dr}=\frac{q(r)}{\varepsilon}
\end{eqnarray}
|
Gauss's Law(又は磁界の場合Ampere's Law)より、r=aの位置で以下の関係があることは既に紹介してきました。
|
\begin{eqnarray}
D=-\varepsilon\frac{dV}{dr}=\frac{Q}{2\pi a}
\end{eqnarray}
|
Preceding Page
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method