 Electromagnetics and Ham Radio
Electromagnetics and Ham Radio
Coaxial15

■計算例その3: 外側の導体が長方形の場合■
例えば、外側のアルミ角パイプを25mm×30mm×3mmに変更したらどうなるか、計算してみました。
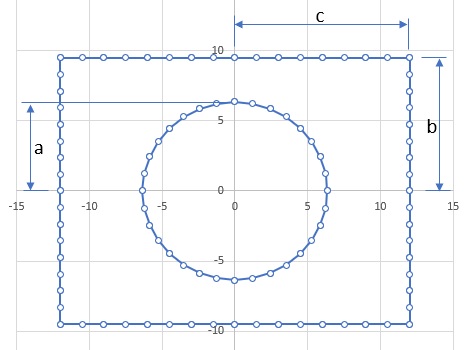
要素分割の状況を下図に示します。要素数は前の例題と同じです。
計算で用いる数値は、a=6.35, b=9.5, c=12になります。
データ作成はプログラム
SETCOAXIAL-OUTER-RECTANGULAR.FOR
が行ってくれます。
このプログラムを実行すると、ファイル
BOUNDARY.DAT
と入力データ
BEM2.DAT
を作成します。
次に2次要素の境界要素法の解析プログラムBEM8QUDQ.FORを実行すると、結果ファイル
BEM2.SOL
を出力します。その他ファイルECHOPRT.SOLも出力します。これは、入力データを
読み易くするためのファイルです。計算結果に不道理な箇所があったときに、
入力データをチェックできます。
 計算を実施すると、半径a上でのポテンシャルは平均でV(a)=0.091531166でした。
特性インピーダンスは、Z0=60×2π×0.091531166=34.51Ωです(π=3.14159...のパイです)。
もう少し計算結果を詳しく見ることにします。
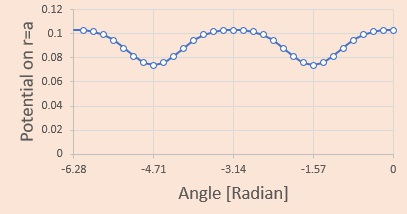
まず、半径r=aの丸パイプ上のポテンシャルですが、以下のような値になります。
丸パイプが角パイプに一番接近する位置(上側と下側)で最小になり、一番遠くなる左と右側で高くなっています。
正方形の角パイプの時とは違ったポテンシャルの分布になっています。
計算を実施すると、半径a上でのポテンシャルは平均でV(a)=0.091531166でした。
特性インピーダンスは、Z0=60×2π×0.091531166=34.51Ωです(π=3.14159...のパイです)。
もう少し計算結果を詳しく見ることにします。
まず、半径r=aの丸パイプ上のポテンシャルですが、以下のような値になります。
丸パイプが角パイプに一番接近する位置(上側と下側)で最小になり、一番遠くなる左と右側で高くなっています。
正方形の角パイプの時とは違ったポテンシャルの分布になっています。
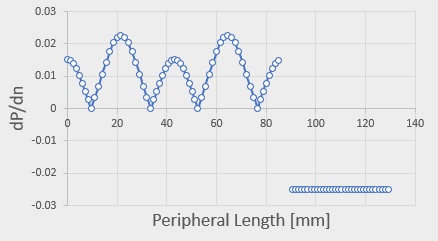
 次にポテンシャルの法線方向の微分∂P/∂nを下に示します。
角パイプの四隅でゼロになっています。角パイプの上側と下側の中央で最大になっています。
次にポテンシャルの法線方向の微分∂P/∂nを下に示します。
角パイプの四隅でゼロになっています。角パイプの上側と下側の中央で最大になっています。
 このように境界要素法を使うと簡単に領域の要素分割ができ、様々な形状の計算が容易にできます。
有限要素法ですと、円の周辺の要素分割に苦労します。
また、境界要素法ではGreen関数を使うため要素分割が少なくても解析精度が向上します。
このように境界要素法を使うと簡単に領域の要素分割ができ、様々な形状の計算が容易にできます。
有限要素法ですと、円の周辺の要素分割に苦労します。
また、境界要素法ではGreen関数を使うため要素分割が少なくても解析精度が向上します。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method


