Electromagnetics and Ham Radio
Coaxial16

■計算領域はフルでなく1/4でも問題ないか？■
上の例題では、丸パイプと角パイプの形状全てを要素で分割しましたが、 対称条件(Natural Boundary Condition)を使うと1/4の領域で計算が出来ます。
例えば例題その3の場合は、以下のような1/4の領域を使って計算できます。 プログラム SETCOAXIAL-OUTER-RECTANGULAR-QUARTER.FOR を実行するとここで必要なファイルを出力してくれます。 入力と結果ファイルについては、上の例題と同じフォーマットですので割愛いたします。

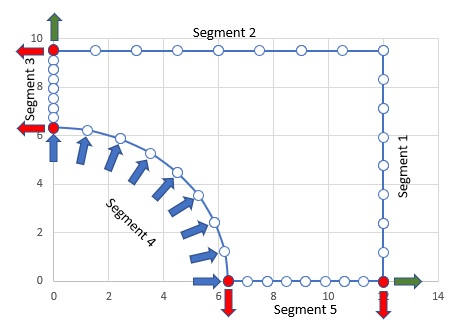この領域にあたっては、5つのセグメントに分割して要素分割を行いました。 境界条件は、セグメント1と2が前の例題と同じDirichlet型で P=0です。セグメント3と5は、自然境界(Natural Boundary Condition)で∂P/∂n=0です。 そして、セグメントと4は前の例題と同じNeumann型のD=∂P/∂n=-0.02506377です。
ここで問題になるのが、上図の赤色●で示した4つの節点です。 これらの節点では、2つの∂P/∂nが存在します。境界要素法では、 角問題(Corner Problem)と言われています。 対処として赤色●の節点を2つの隣接した節点で置き換える という方法があります。 他に、これらの角周辺を短い要素で分割するという方法も考えられます。 いずれにしても角問題(Corner Problem)が無くなるわけではありませんが 計算精度は向上します。ただCorner Problemを完全に取り除く方法がないわけではありません。 それは、一定要素(Constant Element)を使うことです。この要素を使うと、コーナーに節点を置かないので Corner Problemが無くなります。しかし、解析精度が低下してしまいます。 そこで、私が考案したのがハイブリッド要素です。ポテンシャルPである電位(又は磁気ベクトルポテンシャル)を1次要素で、 その微分∂P/∂nを一定要素(Constant Element)で解きます。こうすることで、精度とCorner Problem を解決できます。後ほど計算例を紹介します。
次の図を見て下さい。∂P/∂nを周長に沿ってグラフにしてあります。起点は、上図の右下の 赤丸●です。

Preceding Page Next Page
Menu Inductance Capacitance Z0 Exp Balun Coaxial Off center fed DP Helmholtz FEM BEM
Internet College of Finite Element Method