Electromagnetics and Ham Radio
Balun23
Page 23
■誘電体を含むキャパシタンスの解析■
測定結果から特性インピーダンスに影響を与えているのは誘電体であることが判明したとなると、それなりの数値モデルで検証する必要があります。
このように複数の誘電体が入り込んだモデルの場合、境界要素法で解析するには比誘電率毎に計算領域を分割しなければなりません。
領域分割は境界要素法にとって不得意分野になりプログラムもかなり複雑になります。
このような場合、有限要素法が有力になります。1つの要素に１つの比誘電率を与えることが出来るからです。
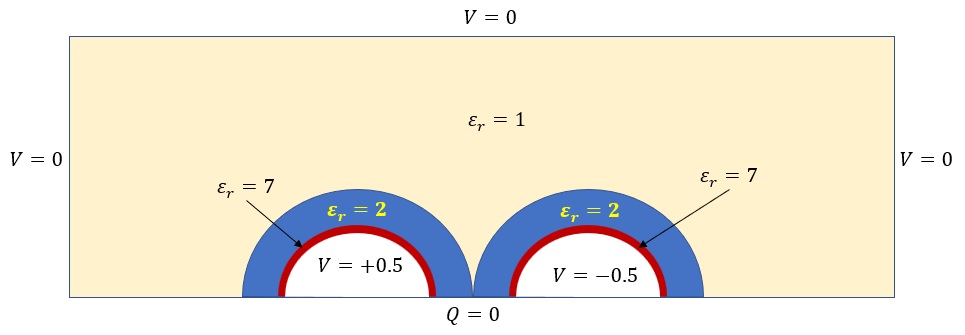
今回の場合、下図のような計算領域を使って境界条件でラプラス方程式を解けば電位分布を解くことができます。
下図の計算領域は、1/2モデルと言って全領域の対称面からの上半分を表しています。対称面にはNatural Boundary condition(自然境界条件)を与えます。
キャパシタンスの計算の場合、Q=0になります。有限要素法の利点はNatural Boundary conditionの面には数値を与える必要がありません。
”何もしない”というのがNatural Boundary conditionなのです。
領域にダブレットがある場合、ダブレットからそう遠くない点でV=0になる可能性がありますが、V=0の位置は出来るだけダブレットから遠ざけた方がよいでしょう。
ラプラス方程式を解く有限要素法のプログラムは本サイトで紹介していますが、入力データの作成に時間が掛ります。
特に、円形の穴が矩形の中に有ると入力データの作成がかなり大変です。境界要素法の場合、このようなデータ作成は簡単なのですが。
いつか時間があるときにこの問題に着手するとし、現段階ではもっと簡単な方法で予測を試みます。
Preceding Page
Next Page
Menu
Inductance
Capacitance
Exp
Z0
Coaxial
Balun
Dielectric
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method
JR2XSO