これまでに、材料の力学特性を示す定数として、E, G, ν が出てきています。前にも述べましたが、材料がIsoTropic(等方性)であると、定数は2つでなくてはならないことが知られています。したがって、Shear modulus(G)は、Eとνの関数として表すことができるはずです。式の展開は、貴方にまかせるとし、ここでは結果のみを下に示します。

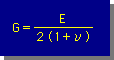
■Matrix 形式による 3次元のStress式の表示法■
有限要素法で弾性解析するためには、Stress式をMatrix 形式で表示する必要があります。まず、Generalized Hooke's Law からStress について解くと、次の様になる。

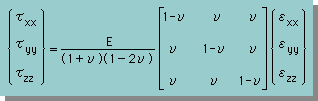
上式へ、せん断応力とShear angleを組み込むと、完全なIsotoropic材料の3次元Stress式が得られます。下式がそうです。

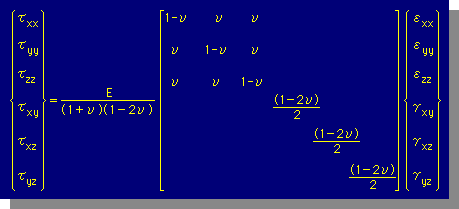
そして、ここでは、上式を次のショートハンドで表すことにします。