支配方程式を導く上では、Stressの式がTensorで書かれていると便利です。Shear strain と Shear angleとの関係が、2εxy = 2εyx = γxy = γyx であることを配慮すると、Stress Tensor は次の様に記述できます。
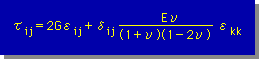
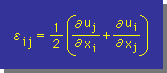 |
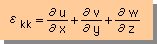 |
|---|
■Strain Gauge■
計算結果のStressと、実物に発生しているStressの比較に、Strain Gaugeが使われます。Strain Gaugeを部材上に張り付け、部材に力を加えると、Strain Gaugeの電気的な抵抗は、ひずみに応じ変化します。つまり、Strain Gaugeの抵抗を測定することにより、Gaugeを張り付けた方向のNormal strain を知ることができます。
しかし、1つのStrain Gaugeの読みから、Stressを求めることは、出来ません。なぜなら、Stressは、
Genralized Hooke's law で示した様に、全てのεiiに関係しているからです。
では、Young's modulus と Poisson's ratio がわかっていたとして、ある表面上の1点の主応力を知りたい場合、何枚のStrain Gaugeを張れば、目的が達成できるでしょうか。
答えは、3つです。または、Rosetteを1つです。下の図を見て下さい。
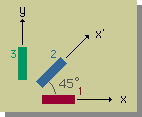
上図は、Gauge間の角度が45度のRosetteです。Gauge1でεxx、Gauge2でεx'x'、Gauge3でεyyが測定出来ます。これらのStrainをMohr's circleから導き出される次の式に代入し、εxyを求めることが出来ます。
| εx'x'=0.5*(εxx+εyy)+0.5*(εxx-εyy)cos2θ+εxysin2θ |
ここに、θ=45度です。
εxyが求まれば、 主ひずみのε1とε2は、簡単に得られる。Strain Gaugeを張った面に垂直な方向のStressはゼロ(τ3=0)ですから、これらの計算された主ひずみをGenralized Hooke's lawに代入すると、主応力が求まります。
解析と実測のStressを比較しようとすると、Rosetteを沢山張り付けるなければならないため、実験が高価になります。そこで、 一般には、解析により得られたStrainと実測のStrainを比較するのが経済的で好まれる方法です。
| BACK | NEXT Failure |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |