上表のdivVとは、前述のように、応力の式にあるε_kkのことです。また、λdivV/EはλdivVをYoung係数で割って数値を無次元化してあります。更にポアソン比の下限値がゼロでないのは、logでグラフ化するためです。そこで、上表のE/λの対数を横軸に、divVとλdivV/Eの対数を縦軸にグラフを描くと下図が得られます。

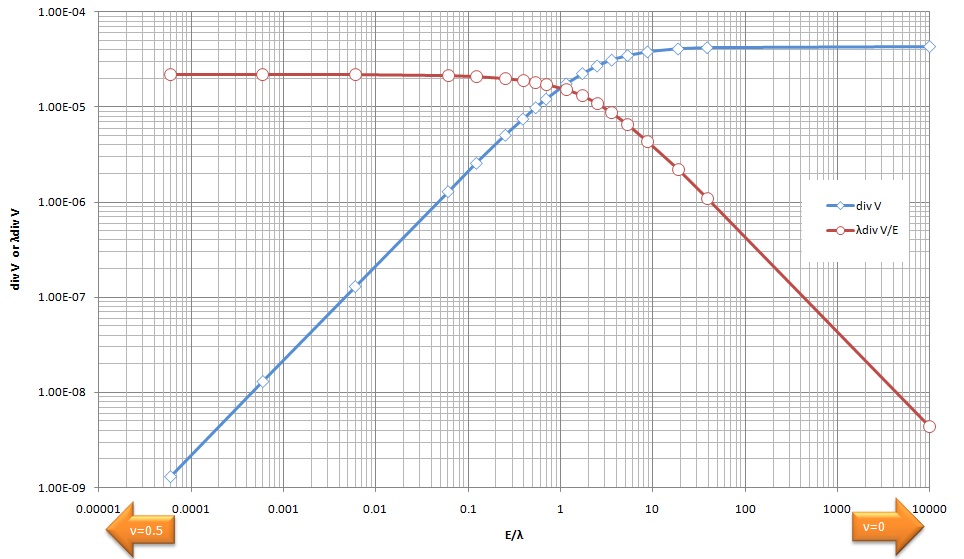
ここでdivVは節点1での値です。他の節点でのdivVをプロットしても同じ様なグラフになりました。また、λの項をフル積分で計算してみましたが、上図に似た形にはなりましたが、ポアソン比が0.5付近で計算が安定しませんでした。 図を見ると、λが大きく(E/λが小さく)なるとdivVが小さくなってゆくのが分かります。その部分の勾配がマイナス1になっています。つまり、ν=0.5付近ではdivV∝1/λの関係にあることがグラフから読み取れます。また、λがゼロ(つまりν=0)において、divVはある値に収束します。ところで、λdivVですが予想通りλが大きくなるとある値に収束しています。そして、λ=0ではλdivV=0になっています。 最初の推論通りにλε_kkはある値に収束します。では、もしポアソン比νが0.499999の材料があるとすれば、どのような変形をするのでしょうか。 同じYoung係数Eでのポアソン比νが0.5に近づくとビームは硬くなりますが、剛体になることはありません。剛体にするには、Young係数Eを無限大にする必要があります。では、アソン比νが0.5またはεkkがゼロになるということは何を意味しているのでしょうか。ビームの体積が力を受ける前と後で変化が無いということです。つまり、流体で言う非圧縮性です。羊羹やこんにゃくがν=0.5になっていると思われます。 逆にポアソン比νが0.3ということは(0.5でない)体積の変化を許しているという事を指します。つまり、密度が変化しているということです。 4-noded Iso-parametric要素でν=0.49999からν=0までの計算を試みました。積分方法ですが、λ項に1点法の低減積分を用い、その他の項にGauss-Legendre 2点法のξ=0.57735を使うと、この曲げ問題に関しポアソン比ν=0.499まで正常な計算を行ってくれました。そこで、λ項に2点法低減積分のξ=1を、その他の項に低減積分2点法のξ=0.46を使うと、ポアソン比ν=0.49999までなんとか対応してくれました。しかし、ビームはかなり硬くなってしまいます。 9-noded Iso-parametric要素では、ν=0.499999が限界でした。要素分割を20×200に拡大してもν=0.4999999が限界でした。また、積分点3点法を使った低減精度積分もλに適用してみました。この場合、ξ=0.57735からξ=0.7746の範囲で選択することになります。ξ=0.57735を選択すると、Gauss-Legendre 2点法と同じになります。ここでは、ξ=0.6, ξ=0.65, ξ=0.7, ξ=0.75で計算してみました。全てにおいてν=0.4999まで対応します。更に積分法の9-noded Iso-parametric要素に対するロバスト性についてν=0.3を取り上げ、ξ=0.58からξ=1まで計算を実行しました。結果、収束解と同じRと応力が得られました。したがって、9-noded Iso-parametric要素はかなりロバスト性の高い要素であると言えますね。ここで、ξ=1はシンプソン則を意味します。 ここら辺は、FEMの上級に価しますので、これで終わりにしておきます。弾性解析で修士や博士を得ようと考えている方は、勉強を続けて下さいね。 Reduced Integration Technique ですが、また、流体のところでも出てきます。次は、流体に絡んだ話です。ちょっと、難しくなりますが、少しずつ進めば、きっと理解できます。頑張って下さい。まー、そんなに先を急ぐ必要はないので、ここらへんで一服して下さい。ビールでも飲んで下さい。

ビールと言えば、Milwaukeeです。Wisconsin洲の洲都 Madison から Milwaukeeの中心部に入るころに差し掛かると、右に Milwaukee Brewers の球場が見えてきます(はっきりは見えないかも)。すると、ビール酵母の匂いがしてきます。匂いは、みその酵母と同じです。 知っていましたか。私が小さい頃、味噌は家で作っていました。もちろん材料の大豆とコメも。

次は2次元弾性解析の最後のページです。そのページでは2次元弾性解析で使用したソフトを紹介してあります。参考にして下さい。