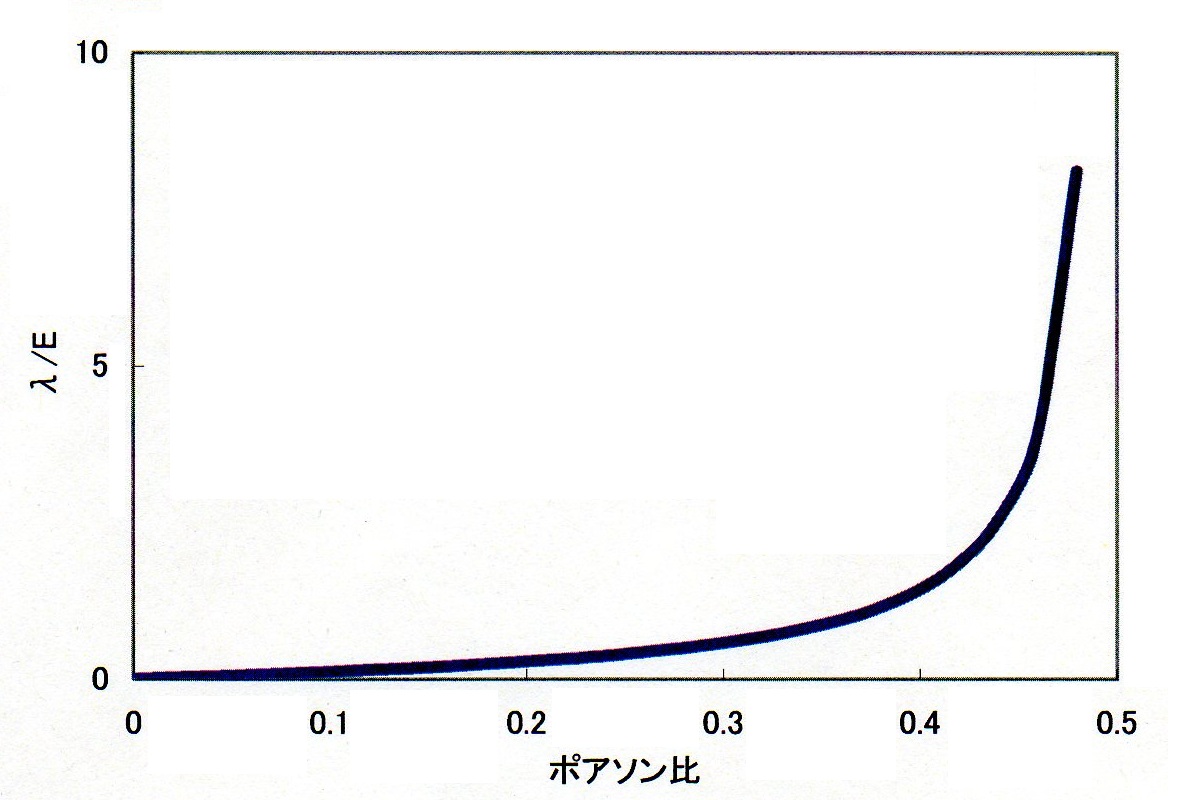
上式から分かるように定数λはポアソン比が0.5で無限大になります。下図を見て下さい。横軸がポアソン比で縦軸がλ/E=ν/((1+ν)(1-2ν))です。ポアソン比が0.5付近で急にλ/Eが大きくなっています。

では、λと掛け算されているε_kkはいったいどうなってしまうのでしょうか。ここに、ε_kkは発散と呼ばれていて、2次元と3次元では以下のように定義されています。また、ここではε_kk以外にdivVも使っています。

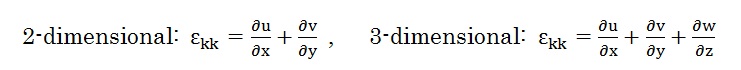
物体に有限な値の力を掛けると、当り前なことですが物体の内部にも有限な値をもつ応力が発生します。ですからλが無限大になったからといって応力が無限大になることはありません。したがってλε_kkはλを大きくしてゆくと、ある有限な値に収束することになります。もちろん、物体の場所によって収束値は違います。ということは、以下のことが予測できます。

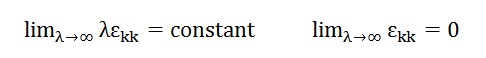
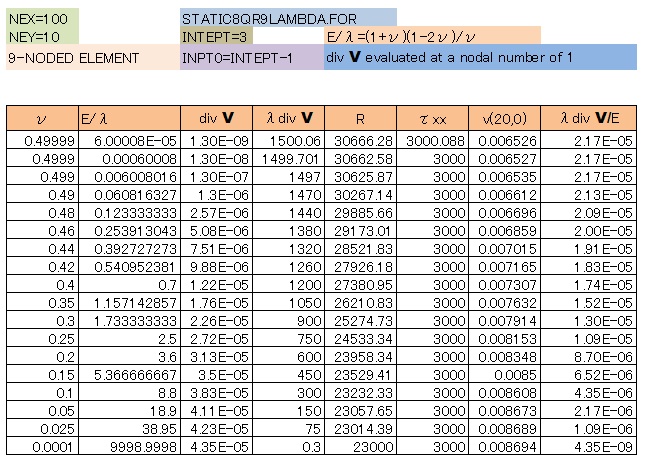
λが大きくなるときλε_kkがある値に収束するということは、ε_kk∝1/λということになりますね。 実際にビームを10×100(NEY×NEX)の9-noded Iso-parametric要素で分割し、ポアソンを0〜0.499999まで計算してみました。使用したプログラムにはλの項に積分点数が１つ少ない低減精度積分法を適用してあります。流体解析の経験からλの項を低減精度積分すると計算が安定することが知られています。計算結果を下表にまとめておきました。