そして、積分点の位置(ξ)を縦軸に、無次元量(r)を横軸にしてグラフにすると、下図が得られます。
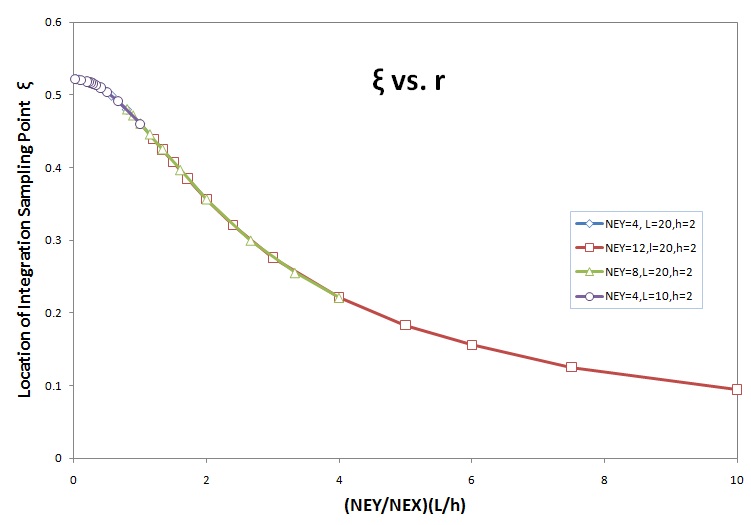
興味深いことに上のグラフが示すように全ての積分点の位置(ξ)は1つの曲線に載ってきます。無次元量(r)がゼロに近づくとξ=0.5216に収束しそうです(NEY=4, NEX=4000の場合)。また、無次元量(r)が無限大では、ξ=0に収束しそうです。つまり、Gauss-Legendre 1点法です。結果的に、以下が言えそうです。参考までに、Gauss-Legendre 2点法の積分点の位置はξ=0.577350269です。
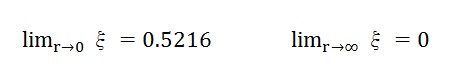
上のグラフが何を意味しているかというと、例えば、計算領域の大きさ(Lとh)と4-noded Iso-parametric要素での分割数(NEXとNEY)が大まかに把握できれば、上のグラフから計算で使うξ値を得ることができます。このξ値で計算を実行すると、Shear lockingとHourglassingの無い精度の高い結果が得られます。3次元でも同様な考えが適用できると思います。
■9節点要素(9-noded Iso-parametric)に様々な積分ルールを適用した場合■
4-noded Iso-parametric要素でも良い結果を得る方法が見つかったところで、9節点要素でも積分点の位置を色々変えて計算し、9節点要素の積分点位置に対する安定性を把握しておきます。
9節点要素では通常Gauss-Legendre3点法を使います。この場合、ξ1=-√(3/5), ξ2=0, ξ3=√(3/5),w1= 5/ 9, w2=8/ 9, w3=5/9です。しかし、2次関数を厳密に積分できるという条件を与えると、1≧ξ3≧√(1/3)から選択できます。ただし、ξ3=√(1/3)を選択するとGauss-Legendre2点法になってしまいHourglassingが発生するので、ξ3>√(1/3)とします。Gauss-Legendre 3点法の代わりに、1≧ξ3>√(1/3)から選択しFree selection 3点法でRの計算を行ったところ、小数点以上は、全て同じ値でした。9節点要素はかなり安定な結果を出す要素と言えます。
このことからも、9節点要素の精度は、要素分割数に左右されないだけでなく、積分ルールにもよらずかなり安定な結果を出す要素と言えます。ロバスト性の高い要素ということになります。
■Poisson's Ratio ν(ポアソン比)が0.499999の場合■
Shear lockingとHourglassingの調査のついでに、Poisson’s Ratioが0.5に限りなく近づいた時の応力と変位はどのように変化するかを調べてみました。応力は、2次元平面歪または3次元の場合、以下の式で書けます。
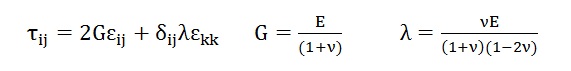
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |