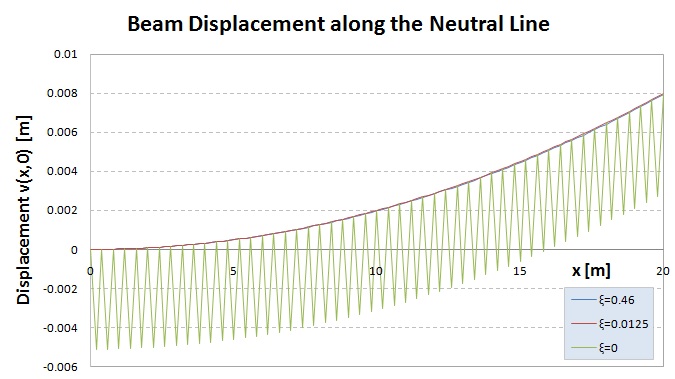
積分点ξの位置がξ=0では、Hourglassing(アワーグラス)が発生したため、変位v(x,0)を表計算ソフトでプロットし目測でRを決定しました。 そのHourglassingですが積分点数が少なくなると発生します。この場合、正規の数2から1つ減らすと顕著に発生します。正規の数とは、与えられた要素を厳密に積分できる積分点数(フル積分点数)のことです。4-noded Iso-parametric要素では、Gauss-legendre 2点法の2、9-nodedと12-nodedではGauss-legendre 3点法の3が正規の数になります。4-noded Iso-parametric要素の場合、Hourglassingは0.57735>ξ≧0の範囲で発生し易くなり、1≧ξ≧57735の範囲では発生しません。下図に示すようにξ=0のときのみ顕著に現れます。

もう少しHourglassingを詳しく見るため、領域の+x面でのu(20,y)を観察してみます。下図を見て下さい。ここに、+x面とは、ビーム先端垂直の境界面を言います。

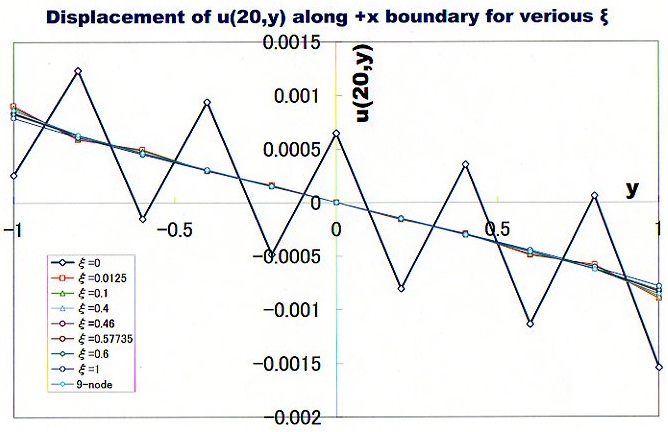
Gauss-Legendre 1点法(矩形公式とも言う)の場合のみ、変位u(20,y)が大きく乱れているのがわかかります。その他全てではかなり安定しているのが上図から読み取れます。しかし、ξ=0以外でどのような状況になっているか詳しく調べるために、9-noded要素で得られた値を収束解とし差をみてみました。下図をご覧下さい。ξ=0の計算結果はスケールから大きく外れるのでプロットしてありません。

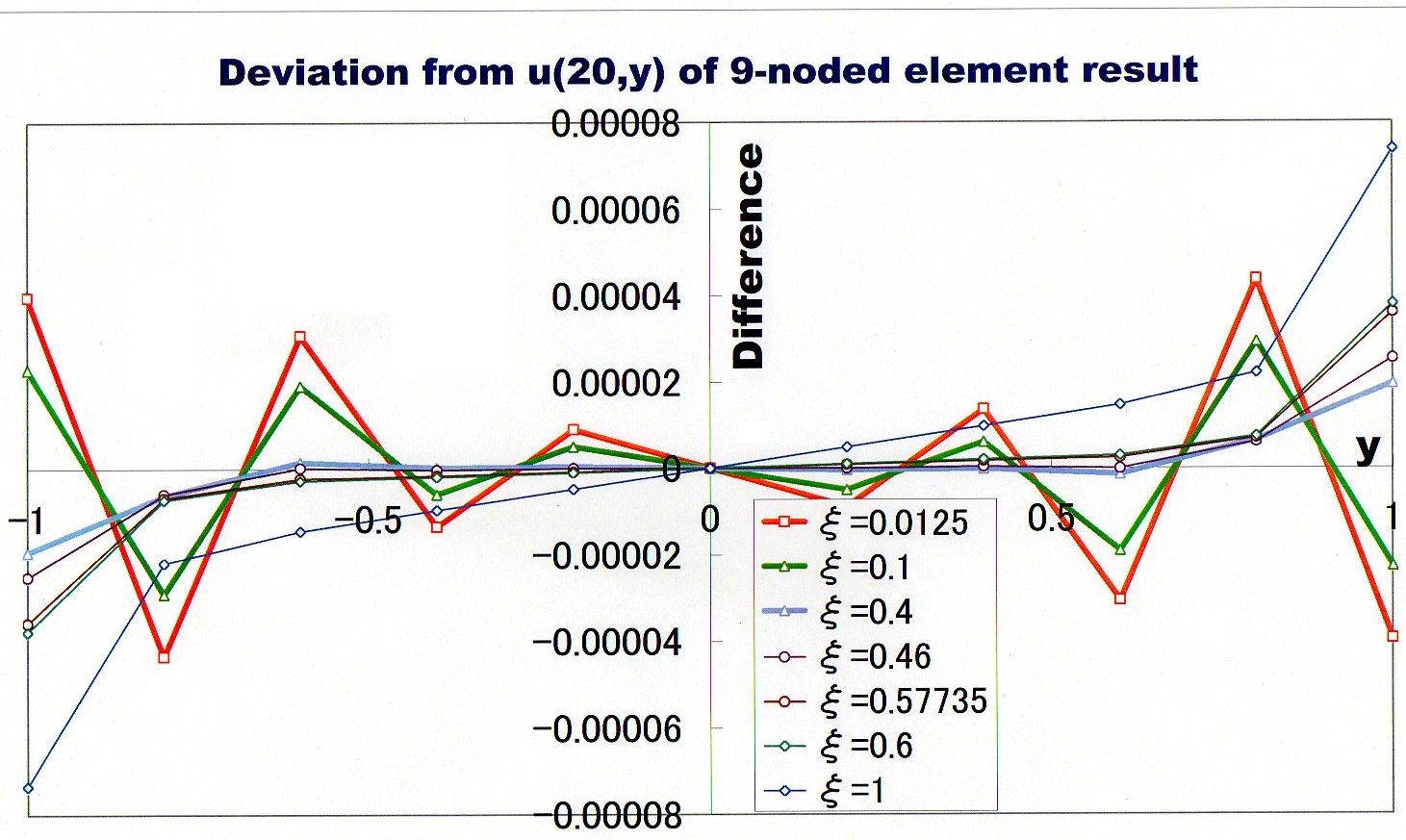
範囲1≧ξ≧0.46ではHourglassingが発生していません。ところが0.46>ξ≧0では変位u(20,y)に乱れが発生しています。 Gauss-Legendre 1点法を使うとHourglassingが発生する理由として、積分で拘束が1つ少なくなったことが挙げられます。積分範囲の真ん中に1点を使って積分するわけですから、積分される関数の傾きに関係なく積分結果は同じになります。市販のソフトで使われたいる積分点数を減らす低減精度積分法(多分)は、Hourglassingの影響をもろにうけるため、Hourglassingを抑制するための制御に苦労しています。ではなぜ積分点数を減らす低減精度積分法を使うのでしょうか。１つのメリットとして考えられるのが、計算時間の低減です。積分点数が少ない分、積分に費やされる計算時間が短くなります。特に時間依存(非定常)の計算には有利になります。しかし、最近の計算機は非常に高速になっていますので積分点数を減らす低減精度積分法を使うメリットは無いように思えます。フル積分点数で非Gauss-Legendre法、つまりFree selection法を使うのが良いかと思いますが。それ以前に2次要素をおすすめします。 話は少々脱線してしまいましたが、4-noded Iso-parametric要素はShear lockingとHourglassingという問題を抱えていることが分かりました。しかし、4-noded Iso-parametricは扱い易い要素です。特に、非定常計算には有用です。私も良く使っています。 では、Shear lockingとHourglassingを発生させなくて尚且つ計算精度を9-noded Iso-parametric要素と同等にすることはできないのでしょうか。これに応えるために領域を様々な数で分割し、更に積分点(ξ)の位置をチューニングしながら常に計算結果のRが9-noded Iso-parametric要素と同値になるようにξを探し出してみました。以下がその計算結果です。下図のL=ビームの長さ、h=ビームの高さ、NEX=ビームの長さ方向の要素分割数、NEY=ビームの高さ方向の要素分割数です。下には、ビームの長さ違いの計算結果も含まれています。

要素分割数とビームの大きさを以下の式で無次元の量(r)で表してみました。実際は以下の式に到達するまでにトライ＆エラーがありました。

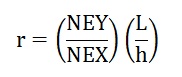
L/NEX=ΔX、h/NEY=ΔYと置けば、上式のrはr=ΔX/ΔYとなり、これは要素のアスペクト比になります。