計算を行う前にインターネットで文献調査をいくつか行いました。それらによると、4-noded Iso-parametric要素は、Shear locking (せん断ロッキング) 現象というやっかいな問題を引き起こすことが知られています。つまり、計算結果の歪が少し硬めに出ます。そしてこの現象を解消する1つの方法にReduced integration 法(低減精度積分法)があります。しかし、この方法はHourglassing現象というまたもややっかいな問題を引き起こすことも知られています。ここでいう低減精度積分法とは、フル精度積分がGauss-Legendre 2点法の場合、Gauss-Legendre 1点法(矩形公式)を使うことを指す。更に文献調査を進めると次の記述がありました。2次を含む高次の要素を使うと、Shear locking現象は殆ど発生しなくなり精度の良い結果が得られます。 そこで文献調査結果を受け、ここでは8-noded, 9-noded, 12-noded Iso-parametric要素を扱えるようにこれまでのプログラムを改良し、4-noded Iso-parametric要素の悪さとShear locking現象およびHourglassing現象を再現してみることにします。そして、Shear lockingとHourglassing現象が無縁で尚且つ高次要素と同等の精度が得られる低減精度積分の1つのFree Selection法を紹介します。
これまでのプログラムSTATIC8Q.FORを含む以下のソフトを開発しました。
| プログラムの名称 | 2G項の 積分 |
G項の 積分 |
λ項の 積分 |
取扱要素 | 連立方程式の 解法 |
|---|---|---|---|---|---|
| STATIC8Q.FOR STATIC8QFXCOMBINE.FOR |
正規 | 正規 | 正規 | 4, 8, 9, 12 | 消去法 |
| STATIC8QFXCOMBINE- LLDECOMP.FOR |
正規 | 正規 | 正規 | 4, 8, 9, 12 | [L][D][L]tDecomposition |
| STATIC8QRXCOMBINE- LAMBDA.FOR |
正規 | 正規 | n-1 | 4 | 消去法 |
| STATIC8QRXCOMBINE- LAMBDA-FREE-SELECTION.FOR |
正規 | 正規 | 正規/non-GL | 4 | 消去法 | STATIC8QRXCOMBINE- SHEAR.FOR |
正規 | n-1 | 正規 | 4, 8, 9, 12 | 消去法 |
Free Selection法で積分する場合は、STATIC8Q.FORまたはSTATIC8QFXCOMBINE.FORの積分ルールを制御しているSubroutine GRULEにある座標値を書き換えるだけですみます。
■Poisson's Ratioの影響■
まずは、Poisson’s ratioが変位に与える影響をみるため、9-nodedと12-noded Iso-parametric要素で様々なPoisson’s ratioを使ってビームが円弧を描く半径( R )を計算してみました。弾性解析で得られた縦方向の変位(v(x,0))を中立軸(y=0の線)に沿って出力させ、最小二乗法で半径Rを計算します。力が作用しているビーム先端付近は、変位が安定しないので、ビームの先端部分(全体の1割)は最小二乗法の計算から除外しました。
計算領域は、縦(NEY)を20要素、横(NEX)を100要素で分割してみました。
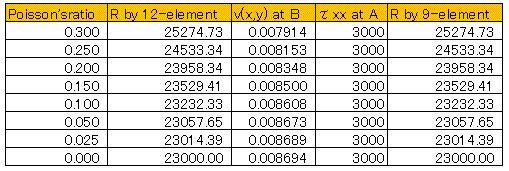
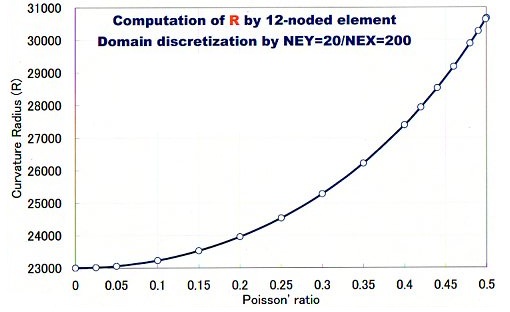
ついでに、点Bでの変位(v(20,0))と点Aでの応力τxxも上の表に載せておきました。計算結果のRを見ると、12節点要素と9節点要素は全く同じ結果を出しています。上の表には有りませんが、変位と応力も両者で同じでした。12節点要素によるRをプロットすると以下のようになります。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |