ここで、Poisson’s ratioの影響が考慮されていない材料力学を用いて諸数値を計算すると以下のようになります。材料力学の本を参考に読者の皆様も計算してみて下さい。

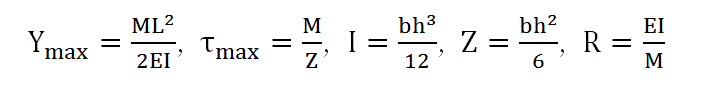
上式より、I=0.66667m⁴, Z=0.66667m³, Y_max=0.008695652m, τ_max=3000Pa, R=23000mとなります。 12節点要素の計算結果のPoisson’s ratioがゼロのときと上の理論解のRとτxxが一致しています。ということで、12節点要素または9節点要素の20X100分割の計算結果を収束解とし今後の計算結果の精度検証に使います。Poisson’s ratioがゼロのケースを取り上げてもλがゼロになってしまいますので、ここからは、Poisson’s ratio=0.3で計算を進めることにします。つまり、ビームの変形はR=25274.73mが厳密解に最も近い値となります。ここでは、収束解と呼ぶことにします。 注意：ここで紹介している計算結果は平面ひずみによるものです。2次元平面応力か3次元で計算すると、どんなPoisson’s ratio を使ってもR=23000m近辺になります。3次元で平面ひずみの計算結果が得られるような長幅ビーム(高層住宅のベランダの様な)で計算すると、Poisson’s ratio=0.3でR=25274mが得られることを確認しています。

■12節点要素と9節点要素の計算精度■
要素数が多いと良い結果を出すことは分かりました。しかし、要素数を少なくしたらどうなりでしょう。そこで、要素分割数を少なくしたとき、これらの要素はどのような特徴を示すかを検証する必要があります。次の2つの図をみて下さい。グラフの横軸(NEX)がx方向の分割数です。縦軸は、半径Rの計算誤差を%で表してあります。誤差の計算式は、(計算値-収束解)/収束解×100です。

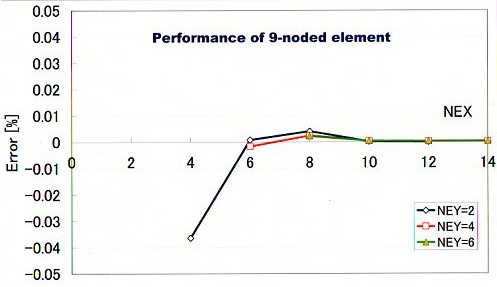
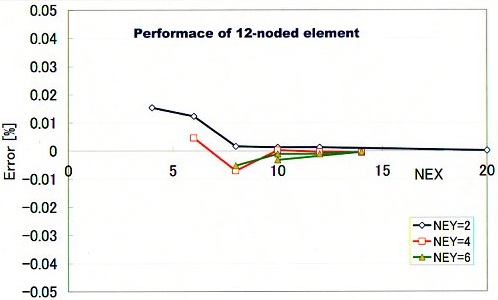
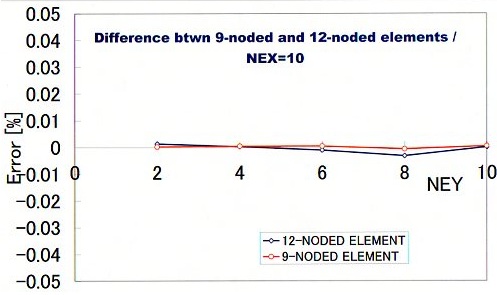
計算領域をかなり粗いNEY×NEX=2×4で分割しても誤差は0.04%以下になっています。かなり精度が高いとという感じです。また、高さ方向の要素分割(NEY)を変えても計算精度に影響を与えていません。つまり、要素分割数に対しロバスト性に優れ精度が高いということです。下図は、横方向の分割数(NEY)を10の固定した場合のRの計算誤差を示します。グラフの横軸はNEYです。