この部材の変形角度は、後程、有限要素式を導くときに使いますが、テンソルで弾性解析の支配方程式を導くときにおいて、γxy は少々不便です。そのため、Shear Strain は、次の様に定義されています。
| εxy = εyx =γxy/2 = γyx/2 |
y と z 軸まわりについても同様に、Shear Angle でShear Strainを書き表すことができる。
結果的に、Normal Strain と Shear Strain を 1つの Second Order Tensor としてまとめることが出来ます。
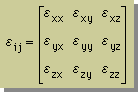
次に、Shear Strain を数値化するために、Shear Strain と変位ベクトルとの関係を調べてみます。 まず、下図を見て下さい。Shear応力が部材ΔxΔyに作用したことにより、y座標軸に面していた部材は、Δyの点でΔu移動しています。同様に、ΔxでΔv移動しています。
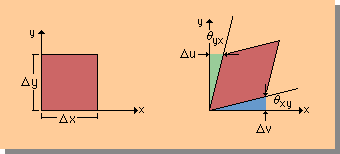
上図の角度θxyとθyxが、非常に小さいとすると、θ=tan(θ)になります。つまり、以下のことが言えます。

したがって、部材ΔxΔyに与えられる Shear Angle (γxy) は、次式で表すことが出来る。
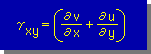
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |