同様に、Shear Strain も次式で計算できます。

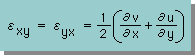
上式の Shear Strain と 前に紹介したNormal Strain が同じ形の式で表されていると、Navierの式等を導く時に非常に便利です。下式を見て下さい。Shear Strain とNormal Strainの両方が満足していることに気付くと思います。

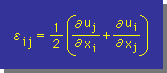
Strain の計算が出来るようになったところで、主ひずみ(Principal Strain)の計算方法について、簡単に触れておきます。下に示す Stress tensor と Strain tensor を比較すると、幾つかの共通点が有ります。両者とも、normal と Shear が有り、対称マトリックスになっています。

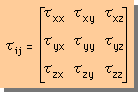Stress Tensor	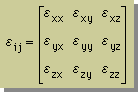Strain Tensor

この共通点を利用すると、Strain も、 Stress 同様、Mohr's Circle を使って主ひずみ(Principal Strain)と最大Shear Strain を求めることが出来ます。

ソフト的には、Stress の主応力の計算をするプログラムが有れば、主ひずみの計算に使えることになります。この時に注意することは、τ_xyの代わりにγ_xyでなくε_xyを代入することです。弾性解析のソフトウエアーパッケージのポスト処理プログラムから算出される項目に、γ_xyがあります。この値を主応力の計算をする関数やサブルーチンに入れても正しい解答は得られません。くれぐれも注意して下さい。