同様に、τ_xx=C-τ_yyとおくと、次の様な円の式が導けます。

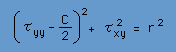座標軸を90度回転すると、τ_xxが回転前のτ_yyと同じ値になることに注意して下さい。つまり、上の式と、その前の式は、同じ作用をする式であることになります。ここでは、円の式をもっと一般化するためにτ_xx or τ_yy = τ_nn、τ_xy = τ_nsとします。

すると次の円の式が出来あがり、この式によって描かれる円をMohr's Circle と言います。

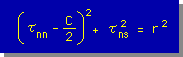
下にMohr's Circleを示します。貴方は、円の大きさと位置を、上の式を見ながら確認して下さい。

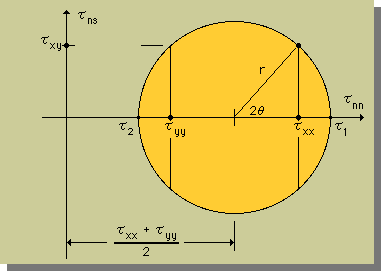
図を参考にすると、主応力τ₁とτ₂と、最大せん断応力を計算する式を、簡単に導き出すことが出来ます。

上の図でもう1つコメントしたいことが有ります。 それは、Mohr's Circle で180度回転すると、実際の部材上のx-y座標系では90度回転するということです。つまり、x-y座標系で座標軸を90度回転すると、τ₁とτ₂が入れ替わります。 このことより、x-y座標系での回転角をθとすると、Mohr's Circle では2θ回転することになります。