次に、どれだけ部材上の座標を回転すると、τnnがτ1とτ2になるかですが。これもMohr's Circleから簡単に導くことができます。下がの式です。
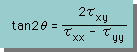
さらに、Mohr's Circleからτx'x' or τy'y'とτx'y'を求める式を容易に導くことができます。τi'j' は、x-y座標からθ回転しているx'-y'座標上の応力を示します。
3次元の主応力も、これまで説明してきた手続きで、求めることができます。3次元の場合、Eigen Value Problemから導き出される式は、3次式になります。そして、同様に座標のオリエンテーションに関係なく不変な定数を導きだすことができます。
Mohr's Circle や 主応力の計算方法について、さらに詳しい情報を知りたい方は、材料力学等の本を参考にして下さい。
■変位(Displacement)■
変位は、部材に力をかけたことによる、部材の内部および表面のある点の移動量を示します。下図のベクトルuが、点Aでの変位です。
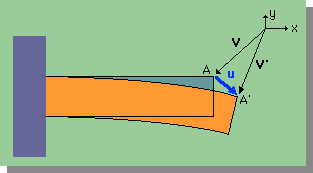
変位は、点A' を表すベクトルV'から点A を表すベクトルVを引くと得られます。つまり、
| u = V' - V |
そして、一般に変位は次の式で表します。
| u = ui+vj+wk |
さらに、テンソルでは変位を、ui で表します。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |