連立方程式は、出来上がりましたが、 τnn は簡単に求まりそうにありません。何故かと言うと、連立方程式の右辺がゼロのベクトルだからです。では、どの様にすればτnn は求まるのでしょうか?。
まず、この問題がトリビアルでないことをチェックします。つまり、anxとanyからなるベクトルがゼロでないことです。確かに、anxとanyの両方が同時にゼロになることはなさそうです。
すると、最後の手段として、前ページに示したマトリックスのDeterminantがゼロでなくてはならないことになります。この様な問題をEigen Value Problem といいます。
マトリックスのDeterminantを計算し、並び換えると次の様になる。
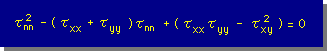
ここに、前に説明したようにτyx=τxy としてあります。
τnnについて上の式を解くと、τ1とτ2が実根として算出されます。判別式で調べると、τ1とτ2は、常に実根であることが分かります。
上の式は、もっと重要な情報を私達に伝えています。つまり、解析条件が変わらない限り、上の式から算出されるτnnは、解析領域の座標軸のオリエンテーションに関係なく不変でなくてはならないということです。
これは、当り前なことですが、かなり重要な事柄です。何故かと言うと、上式の定数も不変でなくてはならないからです。つまり、下図に示す条件が成り立つことになります。
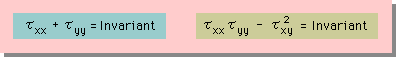
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |