これで、計算に必要な材料は全て揃いました。 次に行うステップとして、上図の三角形の部材のx方向に対しNewton の第2の法則を適応します。つまり、
| ΣFx = max = 0 |
すると次の式が得られます。
| τnnLanx - τnsLany - τxxΔy - τyxΔx = 0 |
ここに、τnnLは、面Lに働いている力、τnnLanxは、τnnLのx成分です。貴方もこの式が正しいことを確認して下さい。
さて、τnnが最大か最小になる条件として、τns = 0 だったので、上式のτnsを取り除きます。すると次式が得られます。
| (τxx - τnn)anx + τyxany = 0 |
同様にΣFy = 0 より、次の式が得られる。
| τxyanx + (τxx - τnn)any = 0 |
2つの式をまとめて連立方程式の形の書くと、次の様になる。
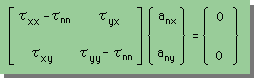
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |