■Boundary Integral■
境界積分(Boundary Integral)では、要素の全表面で起きている事柄を計算し、結果を節点に振り分けます。つまり、離散化ですね。1次元と2次元のところでも説明しましたが、要素の1つが領域内の要素に面している場合、力の釣り合いから、境界積分の結果はゼロになります。よって、領域の境界に面している要素のみが境界積分を行う意味があります。当り前なことですが。

境界積分を行うには、要素の各面ごとに面積分を行います。下は、6面体8-noded要素の1つの面に作用しているTractionを表したいます。

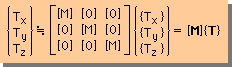
T_x, T_y, T_zは、それぞれその面におけるx,y,z軸方向の外力です。例えば、その面を構成している節点番号が 1,2,3,4 だった場合、T_x, T_y, T_zは次の様になります。

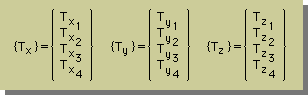
ここに、[M]=[M₁ M₂ M₃ M₄]のことで、各々の形状関数は、x,y,zの関数です。

すると、境界積分は全ての面上で積分を行いますので、以下にに示すSummationが必要になります。

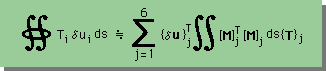
上式中の、{δu}^T_jは、{δu}^T_j={{δu}^T {δv}^T {δw}^T}^Tであって、
{δu}^T={δu_k δu_l δu_m δu_n}であることに注意してください。k,l,m,nはj面上での節点番号を意味します。