■Geometric Matrix■
次にBody force の項の積分を離散化してにてみましょう。この項についても、以前に学んだ通りに作業を進めれば、離散化ができます。ただ違う点は、節点当たりに変数又は未知数が3つ有るということです。 したがって、u_iを6面体8-nodedの要素の形状関数で近似すると、次の様になります。

3次元の変位u_iを表すために、通常の形状関数[N]が3つ必要となります。 ここでは、上式の様に、[N]が3つ入った形状関数を[N]で表すことにします。また、上式を用いて、δu_iも表せられることも出来ます。一応、念のため。

さらに、節点におけるBody force の値を用いると、B_iも同様に、次の様に表すことが出来ます。

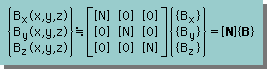
よって、Body force の積分の項は、下式によって離散化が可能になります。

ここでは、ベクトル{B}が出てきましたが、[B]マトリックスとはなんの関係もありません。混同しないで下さいね。